双周赛 Weekly Contest 130
双周赛:https://leetcode.cn/contest/biweekly-contest-130/
100299. Check if Grid Satisfies Conditions
class Solution:
def satisfiesConditions(self, grid: List[List[int]]) -> bool:
n = len(grid)
m = len(grid[0])
for j in range(m):
for i in range(n):
if j != m-1 and grid[i][j] == grid[i][j + 1]:
return False
if i != n-1 and grid[i][j] != grid[i + 1][j]:
return False
return True
100302. Maximum Points Inside the Square
class Solution:
def maxPointsInsideSquare(self, points: List[List[int]], s: str) -> int:
sl = []
for c in s:
sl.append(c)
# print(sl)
n = len(points)
pl = [0] * n
for i in range(n):
x = points[i][0]
y = points[i][1]
pl[i] = max(abs(x), abs(y))
# print(pl)
ps = zip(pl, sl)
sortedPS = sorted(ps, key=lambda p: p[0])
res = 0
# curlen = 0
# curCnt = 0
breakLen = float("inf")
clist = []
for s in sortedPS:
if s[1] in clist:
breakLen = s[0]
break
else:
clist.append(s[1])
for s in sortedPS:
if s[0] < breakLen:
res+=1
else:
break
return res
灵神写法:从集合论到位运算,常见位运算技巧分类总结
- 字典统计
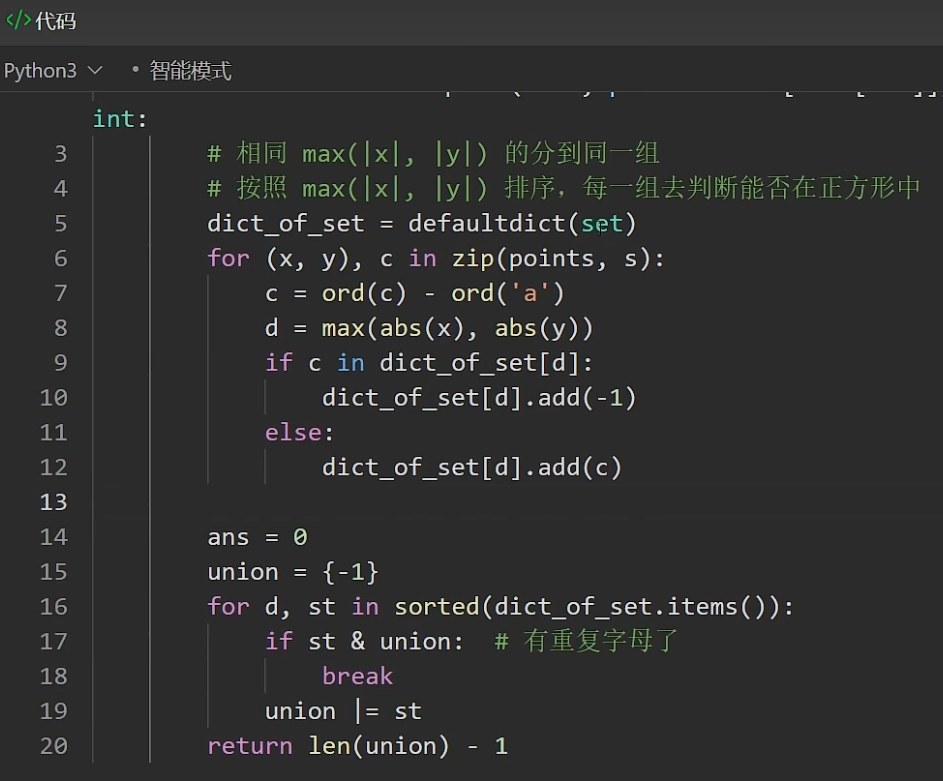
- 位运算
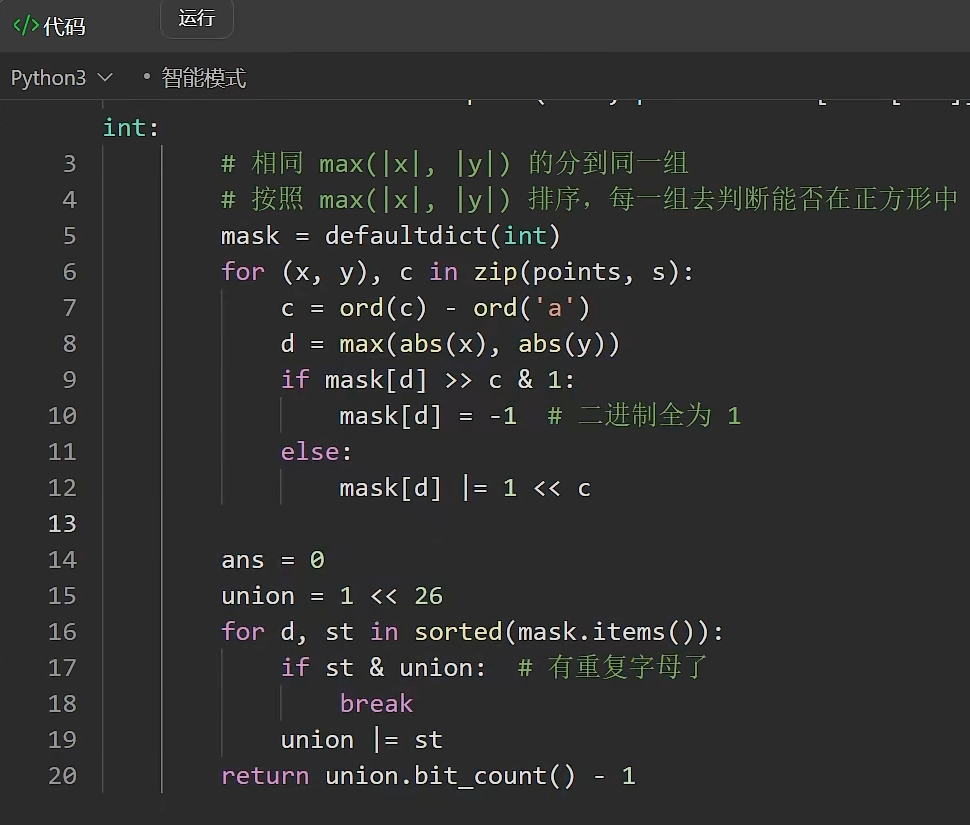
100289. Minimum Substring Partition of Equal Character Frequency
一步一步来,记忆化搜索 timeout;线性递推、优化统计 cnt 方法;优化衡量 balance 方法
1、区间 DP,记忆化搜索,Timeout
- $dfs(0, j) = min(dfs(0, j), dfs(i, k) + dfs(k + 1, j)$ 时间复杂度为 $(n^3)
class Solution:
def minimumSubstringsInPartition(self, s: str) -> int:
s = [ord(s[k]) - ord("a") for k in range(len(s))]
cntDP = []
@cache
def isBalanced(i, j):
if i == j:
return True
cnt = [0] * 26
for k in range(i, j + 1, 1):
cnt[s[k]] += 1
maxCnt = cnt[s[i]]
for i in range(26):
if cnt[i] != 0 and cnt[i] != maxCnt:
return False
return True
@cache
def minBalanceNum(i, j):
if isBalanced(i, j):
return 1
minCnt = j - i
for k in range(i, j + 1, 1):
if k == i:
if isBalanced(k + 1, j):
minCnt = min(minCnt, 1 + minBalanceNum(k + 1, j))
elif k == j:
minCnt = min(minCnt, minBalanceNum(i, k - 1) + 1)
else:
if isBalanced(k, j):
minCnt = min(minCnt, minBalanceNum(i, k - 1) + 1)
if minCnt == 2:
break
return minCnt
return minBalanceNum(0, len(s) - 1)
2、一维线性递推、优化统计 cnt 方法
- 把 isbalance 函数中的
Cnt 数组计算移到上一层遍历中。 - 并且把第一层的记忆化搜索改成一维 dp 递推:$f(i) = minf(j) + 1$
时间复杂度从
approach 1的 $O(n^3) 降到 $(26*n^2)
@cache
def isBalanced(i, j):
if i == j:
return True
# ===== Cnt 数组计算 Start
cnt = [0] * 26
for k in range(i, j + 1, 1):
cnt[s[k]] += 1
# ===== Cnt 数组计算 End
maxCnt = cnt[s[i]]
for i in range(26):
if cnt[i] != 0 and cnt[i] != maxCnt:
return False
return True
完整实现
class Solution:
def minimumSubstringsInPartition(self, s: str) -> int:
n = len(s)
s = [ord(s[k]) - ord("a") for k in range(n)]
def isCntBalanced(cnt):
maxCnt = max(cnt)
for i in range(26):
if cnt[i] != 0 and cnt[i] != maxCnt:
return False
return True
dp = [i + 1 for i in range(n)]
cnt = [0] * 26
for j in range(n):
cnt[s[j]] += 1
if isCntBalanced(cnt):
dp[j] = 1
continue
tmpCnt = cnt.copy()
for i in range(j):
tmpCnt[s[i]] -= 1
if isCntBalanced(tmpCnt):
dp[j] = min(dp[j], dp[i] + 1)
if dp[j] == 2:
break
return dp[n - 1]
3、优化衡量 balance 方法
思路:
- 从后往前维�护 cnt 数组,只用遍历一次
- 计算 maxCnt 和 maxCntChars,用来快速比较 i 到 j 是否 balance
- If 当前 i 的字母 s[i] 的 cnt 大于 maxCnt。更新 maxCnt,并且把 maxCntChars 设置为 1。因为满足 maxCnt 的字母当前只有 s[i]
- else, 如果当前 i 的字母 s[i] 的 cnt 等于 maxCnt。maxCntChars += 1。因为当前字母一定不是已满足 maxCnt 的字母,是一个刚满足 maxCnt 的字母。
class Solution:
def minimumSubstringsInPartition(self, s: str) -> int:
n = len(s)
s = [ord(s[k]) - ord("a") for k in range(n)]
dp = [i + 1 for i in range(n)]
for j in range(n):
maxCnt = 0
maxCntChars = 0
cnt = [0] * 26
for i in range(j, -1, -1):
cnt[s[i]] += 1
if cnt[s[i]] > maxCnt:
maxCnt += 1
maxCntChars = 1
elif cnt[s[i]] == maxCnt:
maxCntChars += 1
if maxCntChars * maxCnt == j - i + 1:
if i == 0:
dp[j] = 1
else:
dp[j] = min(dp[j], dp[i-1] + 1)
return dp[n - 1]