双指针 Opposite Double Pointer
Idea
May need to sort the array in ascending order
- Brute Force Solution only get O(1) info in O(1) time
- Double Pointer Solution takes O(1) time to konw O(n) info, without checking the rest O(n)
Template - 3Sum
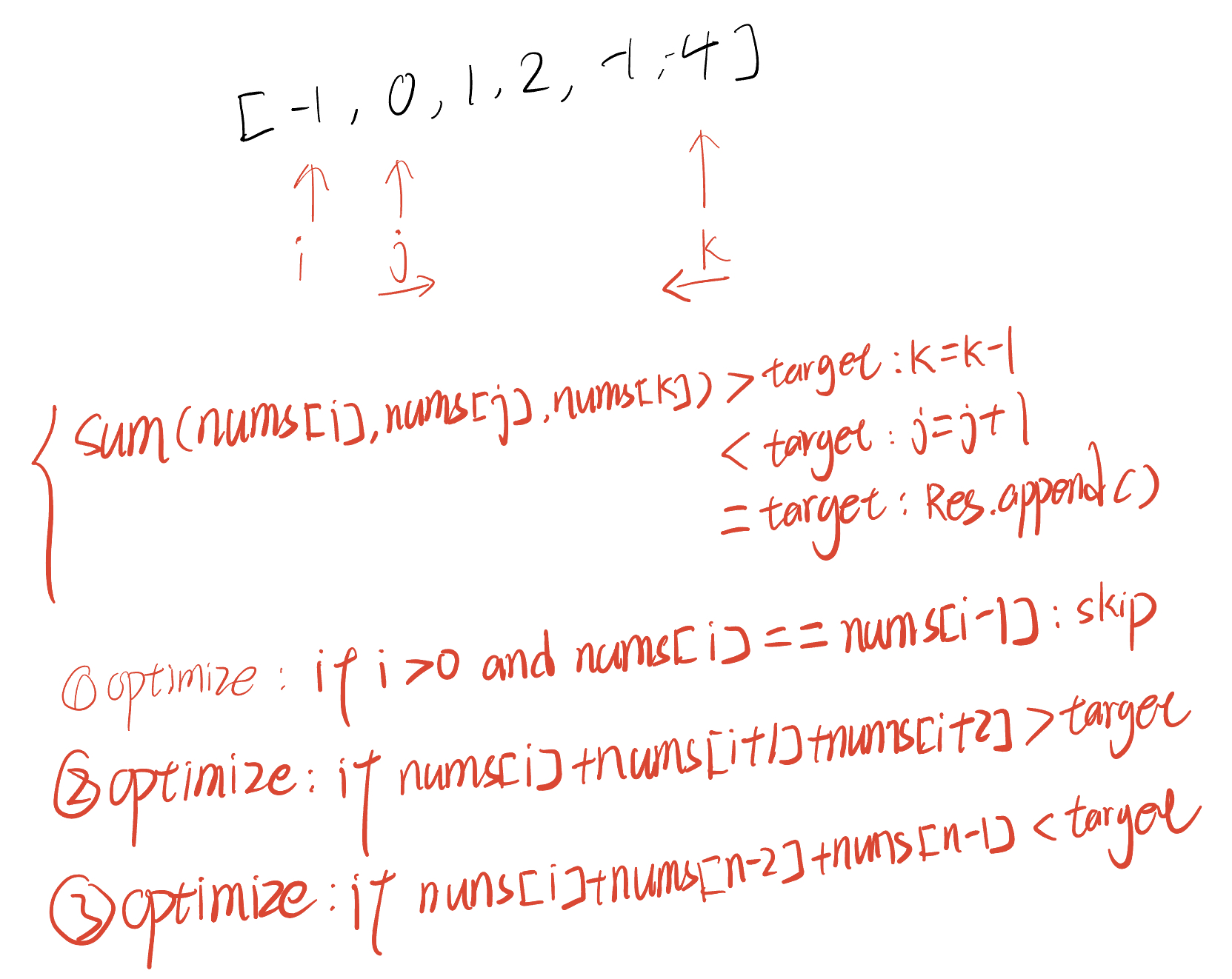
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums = sorted(nums)
res = []
for i in range(len(nums) - 2):
# optimize 1, skip repeat nums[i]
if i > 0 and nums[i - 1] == nums[i]:
continue
# optimize 2, skip impossible number
if nums[i] + nums[i + 1] + nums[i + 2] > 0:
break
# optimize 2, skip impossible number
if nums[i] + nums[len(nums) - 1] + nums[len(nums) - 2] < 0:
continue
j = i + 1
k = len(nums) - 1
while j < k:
curSum = nums[i] + nums[j] + nums[k]
if curSum < 0:
j += 1
if curSum > 0:
k -= 1
if curSum == 0:
res.append([nums[i], nums[j], nums[k]])
# optimize 3, skip same number[j], number[k]
j += 1
while j < k and nums[j - 1] == nums[j]:
j += 1
k -= 1
while j < k and nums[k] == nums[k + 1]:
k -= 1
return res
167. Two Sum II - Input Array Is Sorted
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
i = 0
j = len(numbers) - 1
while i < j:
s = numbers[i] + numbers[j]
if s < target:
i += 1
elif s > target:
j -= 1
else:
return [i + 1, j + 1]
return None
15. 3Sum
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums = sorted(nums)
res = []
for i in range(len(nums) - 2):
# optimize 1, skip repeat nums[i]
if i > 0 and nums[i - 1] == nums[i]:
continue
# optimize 2, skip impossible number
if nums[i] + nums[i + 1] + nums[i + 2] > 0:
break
# optimize 2, skip impossible number
if nums[i] + nums[len(nums) - 1] + nums[len(nums) - 2] < 0:
continue
j = i + 1
k = len(nums) - 1
while j < k:
curSum = nums[i] + nums[j] + nums[k]
if curSum < 0:
j += 1
if curSum > 0:
k -= 1
if curSum == 0:
res.append([nums[i], nums[j], nums[k]])
# optimize 3, skip same number[j], number[k]
j += 1
while j < k and nums[j - 1] == nums[j]:
j += 1
k -= 1
while j < k and nums[k] == nums[k + 1]:
k -= 1
return res
16. 3Sum Closest
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
nums.sort()
n = len(nums)
min_diff = inf
for i in range(n - 2):
x = nums[i]
if i and x == nums[i - 1]:
continue # 优化三
# 优化一
s = x + nums[i + 1] + nums[i + 2]
if s > target: # 后面无论怎么选,选出的三个数的和不会比 s 还小
if s - target < min_diff:
ans = s # 由于��下一行直接 break,这里无需更新 min_diff
break
# 优化二
s = x + nums[-2] + nums[-1]
if s < target: # x 加上后面任意两个数都不超过 s,所以下面的双指针就不需要跑了
if target - s < min_diff:
min_diff = target - s
ans = s
continue
# 双指针
j, k = i + 1, n - 1
while j < k:
s = x + nums[j] + nums[k]
if s == target:
return s
if s > target:
if s - target < min_diff: # s 与 target 更近
min_diff = s - target
ans = s
k -= 1
else: # s < target
if target - s < min_diff: # s 与 target 更近
min_diff = target - s
ans = s
j += 1
return ans
2824. Count Pairs Whose Sum is Less than Target
Brute Force Solution
func countPairs(nums []int, target int) int {
var cnt int = 0
for i := 0; i < len(nums) - 1; i++ {
for j := i+1; j < len(nums); j++ {
if nums[i] + nums[j] < target {
cnt += 1
}
}
}
return cnt
}
Opposite Double Pointer
class Solution:
def countPairs(self, nums: List[int], target: int) -> int:
nums = sorted(nums)
ans = 0
for i in range(len(nums)):
j = len(nums) - 1
while i < j:
if nums[i] + nums[j] < target:
ans += j - i
break
else:
j -= 1
return ans
611. Valid Triangle Number
func triangleNumber(nums []int) int {
sort.Ints(nums)
cnt := 0
for i := 0; i < len(nums) - 2; i++ {
if nums[i] == 0 {
continue
}
x := nums[i]
for j := i+1; j < len(nums) - 1; j++ {
var k int = len(nums) - 1
for j < k {
if x + nums[j] <= nums[k] {
k--
} else {
cnt += k-j
break
}
}
}
}
return cnt
}
11. Container With Most Water
class Solution:
def maxArea(self, height: List[int]) -> int:
left = 0
right = len(height)-1
res = 0
while left < right:
res = max(res, (right-left)*min(height[right], height[left]))
if height[left] < height[right]:
left+=1
else:
right-=1
return res
Prefix Sum
42. Trapping Rain Water

func trap(height []int) int {
res := 0
left := 0
right := len(height) - 1
preMax := 0
sufMax := 0
for left < right {
if height[left] > preMax { //更新preMax
preMax = height[left]
}
if height[right] > sufMax { //更新sufMax
sufMax = height[right]
}
if preMax <= sufMax {
res = res + preMax - height[left]
left++
} else {
res = res + sufMax - height[right]
right--
}
}
return res
}