二叉树与递归,相似平衡 Binary Tree and Recursion v2
100. Same Tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if p == None or q == None:
return p == q
return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
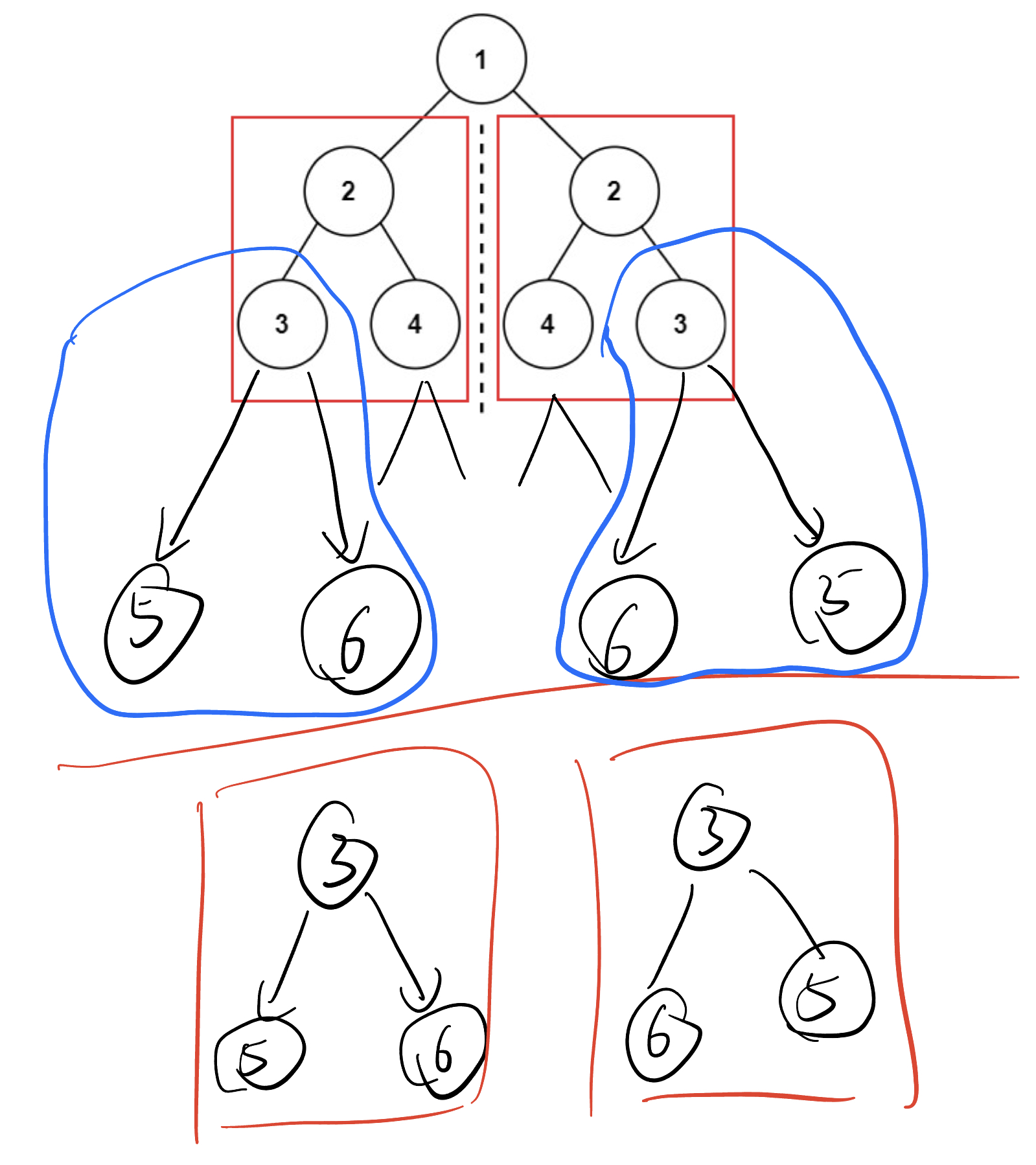
101. Symmetric Tree
要理解递归思路,要知道不管怎么样都可以递归成比较两个子树是否symmetric对称
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if p == None or q == None:
return p == q
return p.val == q.val and self.isSameTree(p.left, q.right) and self.isSameTree(p.right, q.left)
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
return self.isSameTree(root.left, root.right)
110. Balanced Binary Tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def getHeight(p):
if p == None:
return 0
leftHeight = getHeight(p.left)
if leftHeight == -1:
return -1
rightHeight = getHeight(p.right)
if rightHeight == -1:
return -1
if abs(leftHeight - rightHeight) > 1:
return -1
return max(leftHeight, rightHeight) + 1
return getHeight(root) != -1
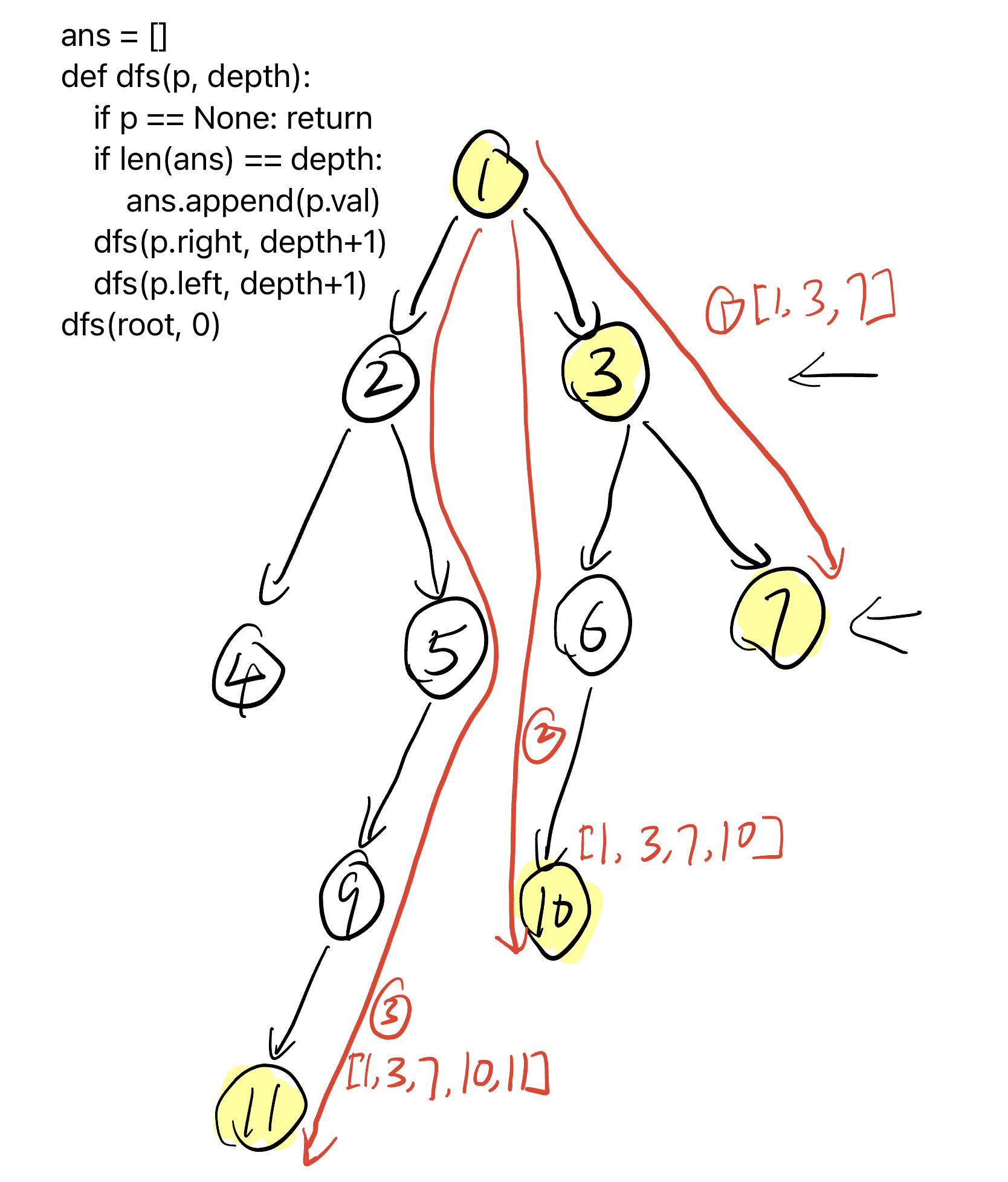
199. Binary Tree Right Side View
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
ans = []
def dfs(p, depth):
if p == None: return
if len(ans) == depth:
ans.append(p.val)
dfs(p.right, depth+1)
dfs(p.left, depth+1)
dfs(root, 0)
return ans