状态机动态规划 State Machine DP
Idea

122. Best Time to Buy and Sell Stock II
class Solution:
def maxProfit(self, prices: List[int]) -> int:
f0 = 0
f1 = -inf
for i, p in enumerate(prices):
new_f0 = max(f0, f1 + p)
f1 = max(f1, f0 - p)
f0 = new_f0
return f0
123. Best Time to Buy and Sell Stock III => At most two transactions
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp=[[[0,0] for i in range(3)] for j in range(len(prices))]
dp[0][1][0]=dp[0][2][0]=0
dp[0][1][1]=dp[0][2][1]=-prices[0]
for i in range(1,len(prices)):
for j in range(1, 3):
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i])
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i])
return dp[len(prices)-1][2][0]
188. Best Time to Buy and Sell Stock IV => At most k transactions
Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
递归要点
- 持有时
hold == 1,卖出dfs(i, j, 0) = max(dfs(i-1, j, 0), dfs(i-1, j - 1, 1) + prices[i]) - 不持有时
hold == 0, 买入dfs(i, j, 1) = max(dfs(i-1, j, 1), dfs(i-1, j, 0) - prices[i]) - 买入或卖出算作一次交易。代码中的
j-1可以是在买股票的时候,也可以��是在卖股票的时候
dfs 递归写法
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = len(prices)
@cache
def dfs(i: int, j: int, hold: bool) -> int:
if j < 0:
return -inf
if i < 0:
return -inf if hold else 0
if hold:
return max(dfs(i - 1, j, True), dfs(i - 1, j - 1, False) - prices[i])
return max(dfs(i - 1, j, False), dfs(i - 1, j, True) + prices[i])
return dfs(n - 1, k, False)
用另一种形式去做边界值也是可以的
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = len(prices)
@cache
def dfs(i: int, j: int, hold: bool) -> int:
# if j < 0:
# return -inf
# if i < 0:
# return -inf if hold else 0
if j == 0:
return -inf if hold else 0
if i == 0:
return -prices[i] if hold else 0
if hold:
return max(dfs(i - 1, j, True), dfs(i - 1, j - 1, False) - prices[i])
return max(dfs(i - 1, j, False), dfs(i - 1, j, True) + prices[i])
return dfs(n - 1, k, False)
递归写法,翻译上面的第一个 dfs 的边界值处理
- 理解为什么是 dfs(n - 1, k, False),因为 k == 0 时是最多交易 0 次,是有意义的。
- 递归中 j 是从 -1 到 k,所以有 k+2 个不同的 j,这个维度是 k+2
- 如果我们把
i == -1当做边界,那需要 handle 从 -1 到 n - 1 的 i,所以有 n+1 个不同的 i,这个维度是 n+1

class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = len(prices)
f = [[[-inf] * 2 for _ in range(k + 2)] for _ in range(n + 1)]
for j in range(1, k + 2):
f[0][j][0] = 0
for i, p in enumerate(prices):
for j in range(1, k + 2):
f[i + 1][j][0] = max(f[i][j][0], f[i][j][1] + p)
f[i + 1][j][1] = max(f[i][j][1], f[i][j - 1][0] - p)
for i in range(n+1):
print(f[i])
return f[-1][-1][0]
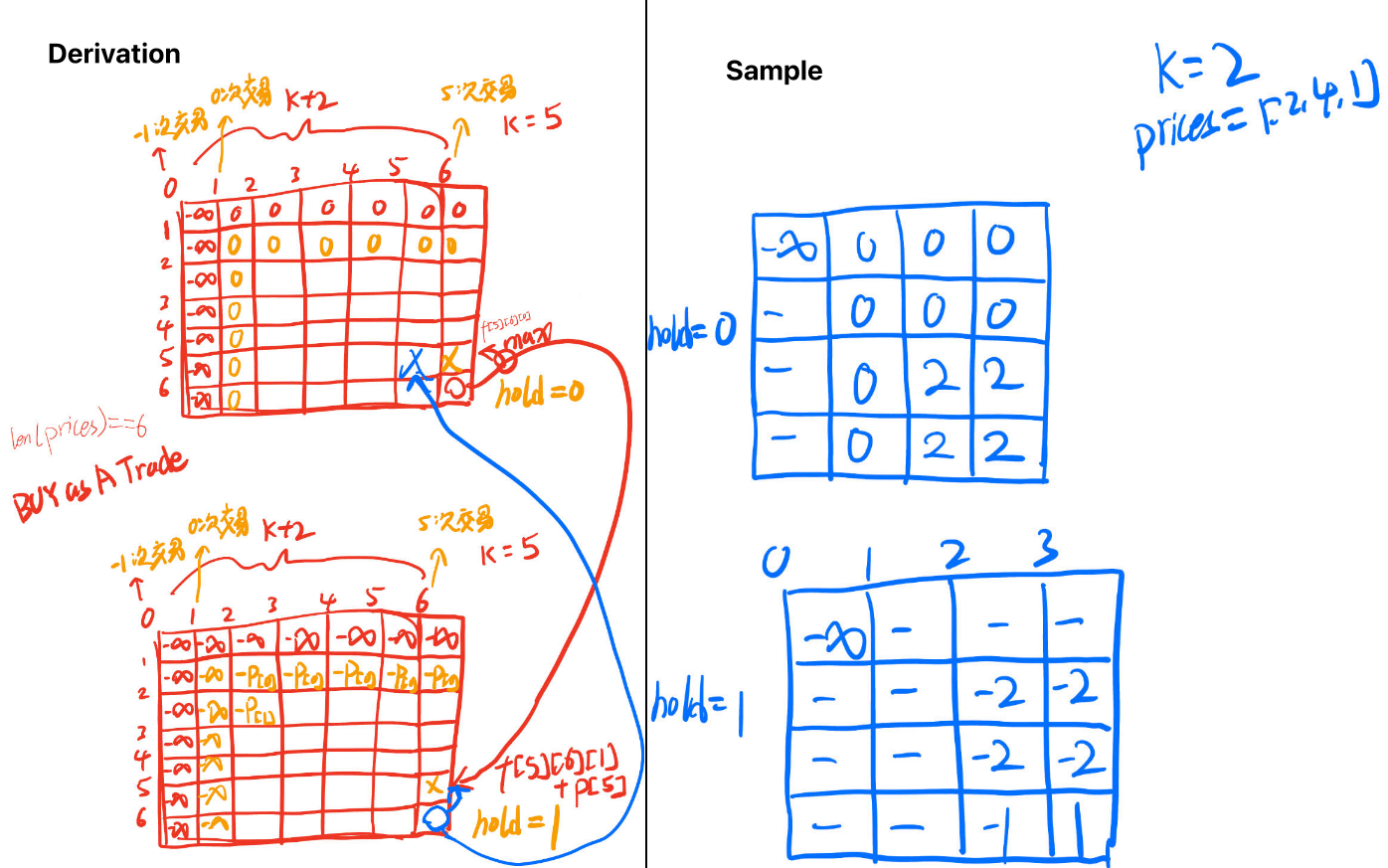
f sample
