Skip to main content

间隔动态规划 Interval DP

516. Longest Palindromic Subsequence​

Palindromic 回文

递归​

区间 DP 是对某个区间 [i, j] 来搜索

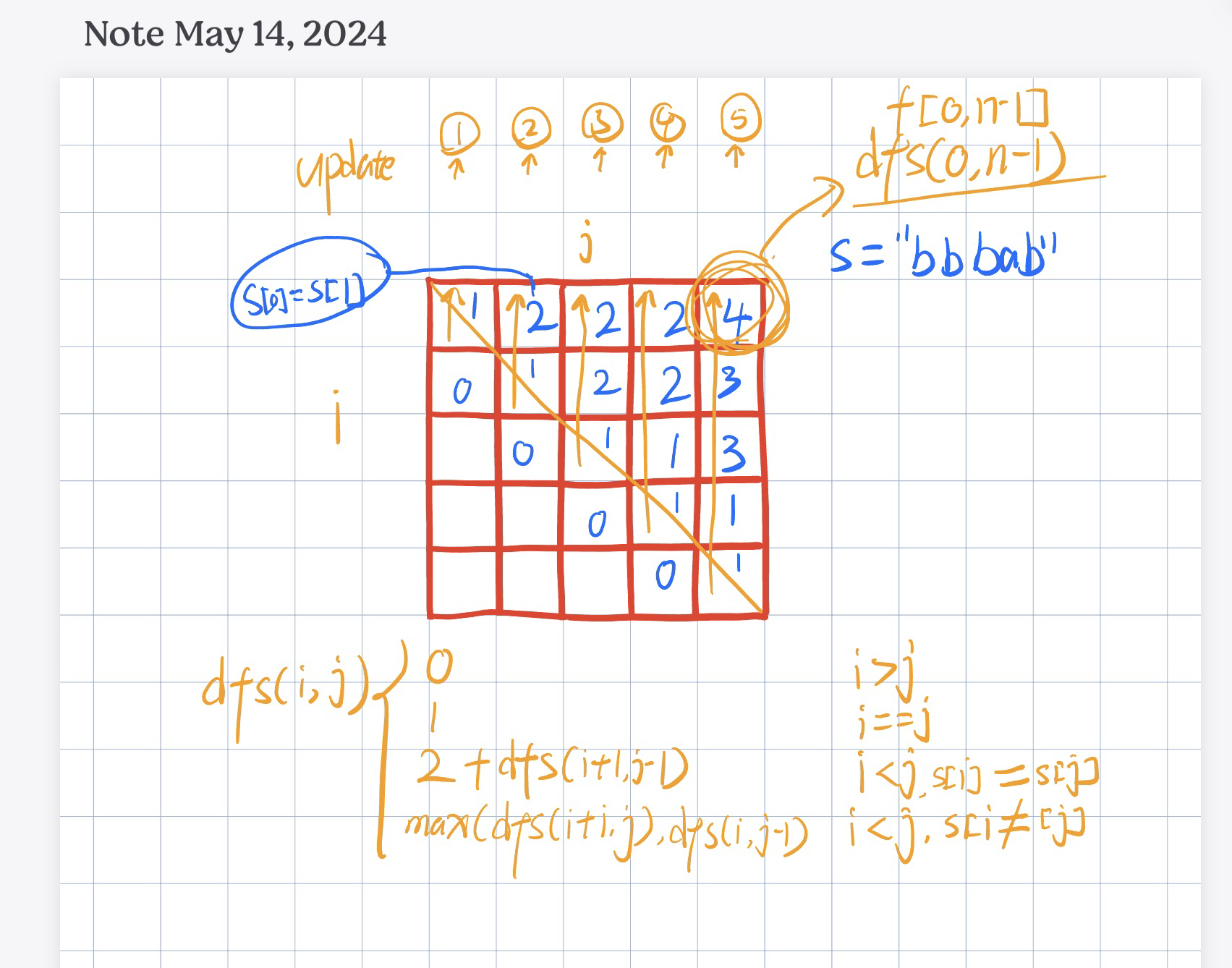
dfs(i, j) =

  • if i > j return 0
  • if i == j return 1
  • if s[i] == s[j] return 2 + dfs(i+1, j-1)
  • return max(dfs(i+1, j), dfs(i, j-1))
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        @cache
        def dfs(i, j):
            if i > j:
                return 0
            if i == j: 
                return 1
            if s[i] == s[j]:
                return 2 + dfs(i+1, j-1)
            return max(dfs(i+1, j), dfs(i, j-1))
        return dfs(0, n-1)

时间复杂度 O(n^2)

  • 动态规划的时间复杂度为：状态个数 X 单个状态的转移次数，此题状态个数为 O(n^2)

空间复杂度 O(n^2)

  • 因为是二维 i, j 记忆化搜索，所以是 O(n^2)

递推​

image-20240514014316409

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [[0 for _ in range(n)] for _ in range(n)]
        for j in range(n):
            for i in range(j, -1, -1):
                if i == j:
                    dp[i][j] = 1
                else: 
                    if s[i] == s[j]:
                        dp[i][j] = 2 + dp[i+1][j-1]
                    else:
                        dp[i][j] = max(dp[i+1][j], dp[i][j-1])
        return dp[0][n-1]

空间优化，两个数组​

考虑到当前 f[i][j] 需要 f[i+1][j-1]，以及 f[i+1][j] 和 f[i][j-1]。可以看出 f[i+1][j-1] 和 f[i][j-1] 都属于前一列f 值，而 f[i+1][j] 属于当前列 f 值。所以状态更新实际上只需要两个数组。

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [[0 for _ in range(2)] for _ in range(n)]
        for j in range(n):
            for i in range(j, -1, -1):
                j2 = j % 2
                if i == j:
                    dp[i][j2] = 1
                else:
                    if s[i] == s[j]:
                        dp[i][j2] = 2 + dp[i + 1][(j2 + 1) % 2]
                    else:
                        dp[i][j2] = max(dp[i + 1][j2], dp[i][(j2 + 1) % 2])
        return dp[0][(n - 1) % 2]

空间优化，一个数组​

因为当前 f[i][j] 计算需要的 f[i+1][j-1] 和 f[i][j-1] 都属于前一列f 值，而 f[i+1][j] 属于当前列 f 值。

如果用一个数组，由于更新 f[i+1][j] 会更新原值 f[i+1][j-1] ，我们可以用一个变量 pre 把 f[i+1][j-1] 存起来

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        n = len(s)
        dp = [0 for _ in range(n)]
        for j in range(n):
            pre = 0
            for i in range(j, -1, -1):
                tmp = dp[i]
                if i == j:
                    dp[i] = 1
                else:
                    if s[i] == s[j]:
                        dp[i] = 2 + pre
                    else:
                        dp[i] = max(dp[i + 1], dp[i])
                pre = tmp
        return dp[0]

Reference​

  1. 区间 DP：最长回文子序列