回溯之子集 Backtrace-Subset

Idea

回溯三问

1. 子问题？
2. 当前操作？
3. 下一个子问题？

Template 78. Subsets

Example

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Template 1

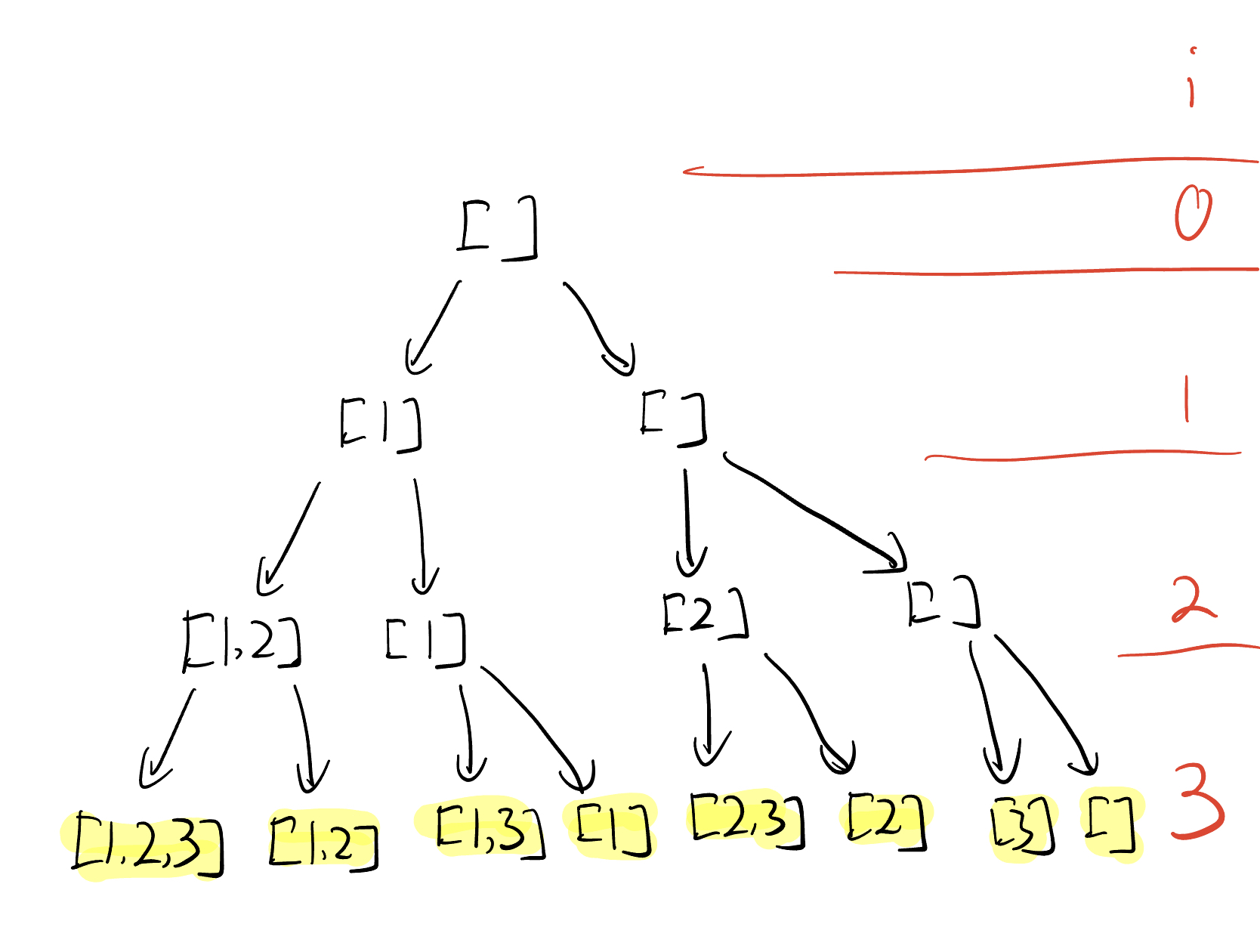
Thinking on the perspective of input, choose or not choose?

• Choose

  path.append(nums[i]) # append current number to path
  dfs(i+1)
  path.pop() # recover path

• Not Choose

  dfs(i+1) # skip current number

Time Complexity: Traverse a Binary Tree O(n^2)

Space Complexity: O(n)

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        if n == 0:
            return []
        
        ans = []
        path = [] # 遍历的路径

        def dfs(i):
            if i == n: # 边界条件。当遍历到叶子节点后生成答案
                ans.append(path.copy()) # 这边使用copy()避免path地址引用改变已生成的结果，这边的copy其实也花了时间
                # ans.append(''.join(path)) # 这是把string类型的数组内容join起来
                return

            dfs(i+1) # 跳过当前数字

            path.append(nums[i]) # 添加到路径中
            dfs(i+1)
            path.pop() # 恢复现场
        dfs(0)
        return ans

Template 2

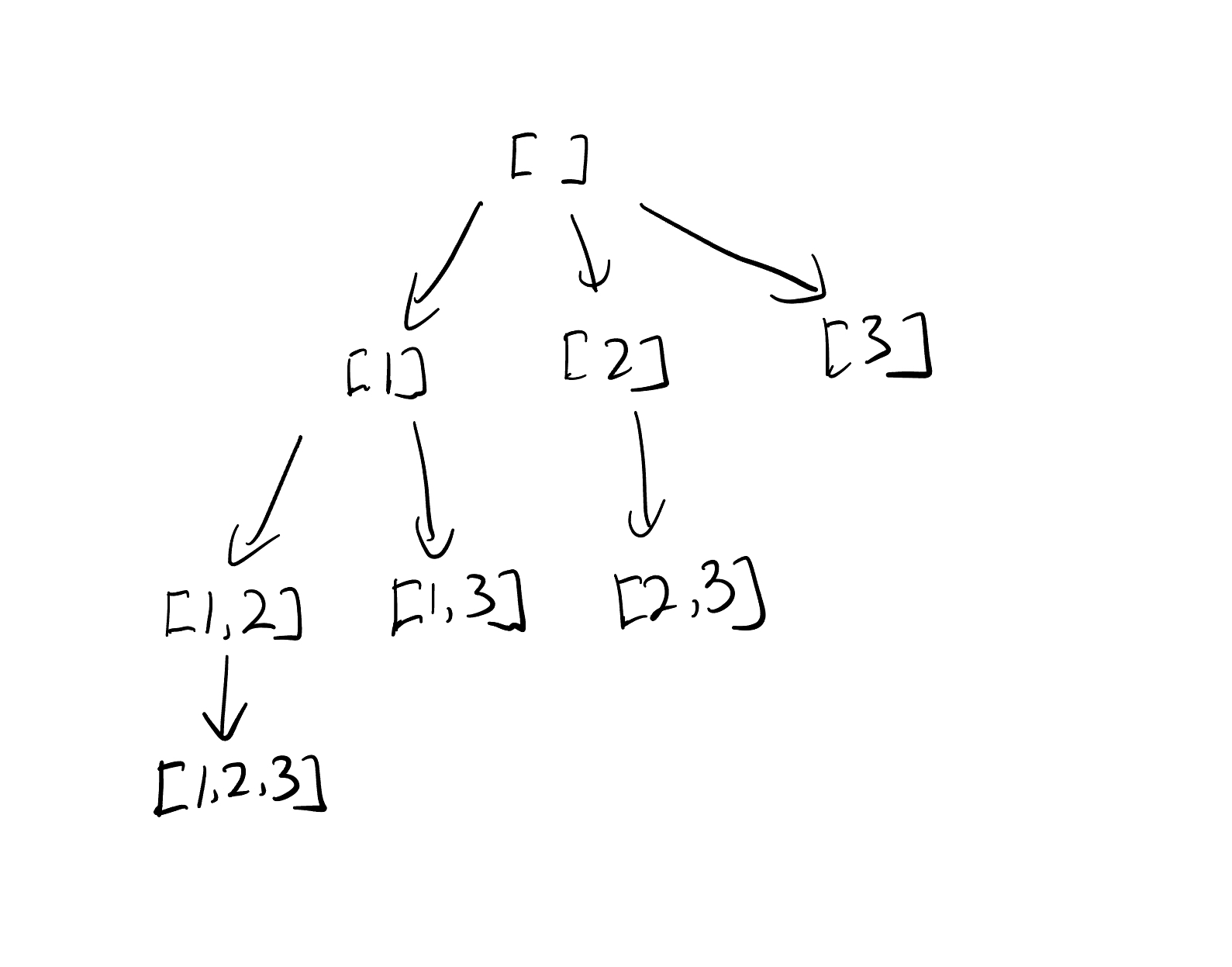
Thinking on the perspective of answer，Which to choose?

• Each node is an answer.

• Traverse every remaining elements at each layer.

Algorithm

1. 子问题？从下标 >=i 的数组中构造子集
2. 当前元素？应该选择满足 j >= i 的 j 元素加入路径
3. 下一个子问题？从下标 >= j+1 的数组中构造子集

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        if n == 0:
            return []
        
        ans = []
        path = [] # 遍历的路径

        def dfs(i):
            ans.append(path.copy()) # 使用copy()避免 path 地址引用改变已生成的结果，这边的copy其实也花了时间
            # ans.append(''.join(path)) # 这是把string类型的数组内容join起来
            if i == n: # 边界条件，返回
                return

            for j in range(i, n):
                path.append(nums[j]) # 添加到路径中
                dfs(j+1) 
                path.pop() # 恢复现场
        dfs(0) # 从零开始
        return ans

Reference

1. 子集型回溯，分割回文串