Skip to main content

图最短路径 Graph V2

单源最短路径​

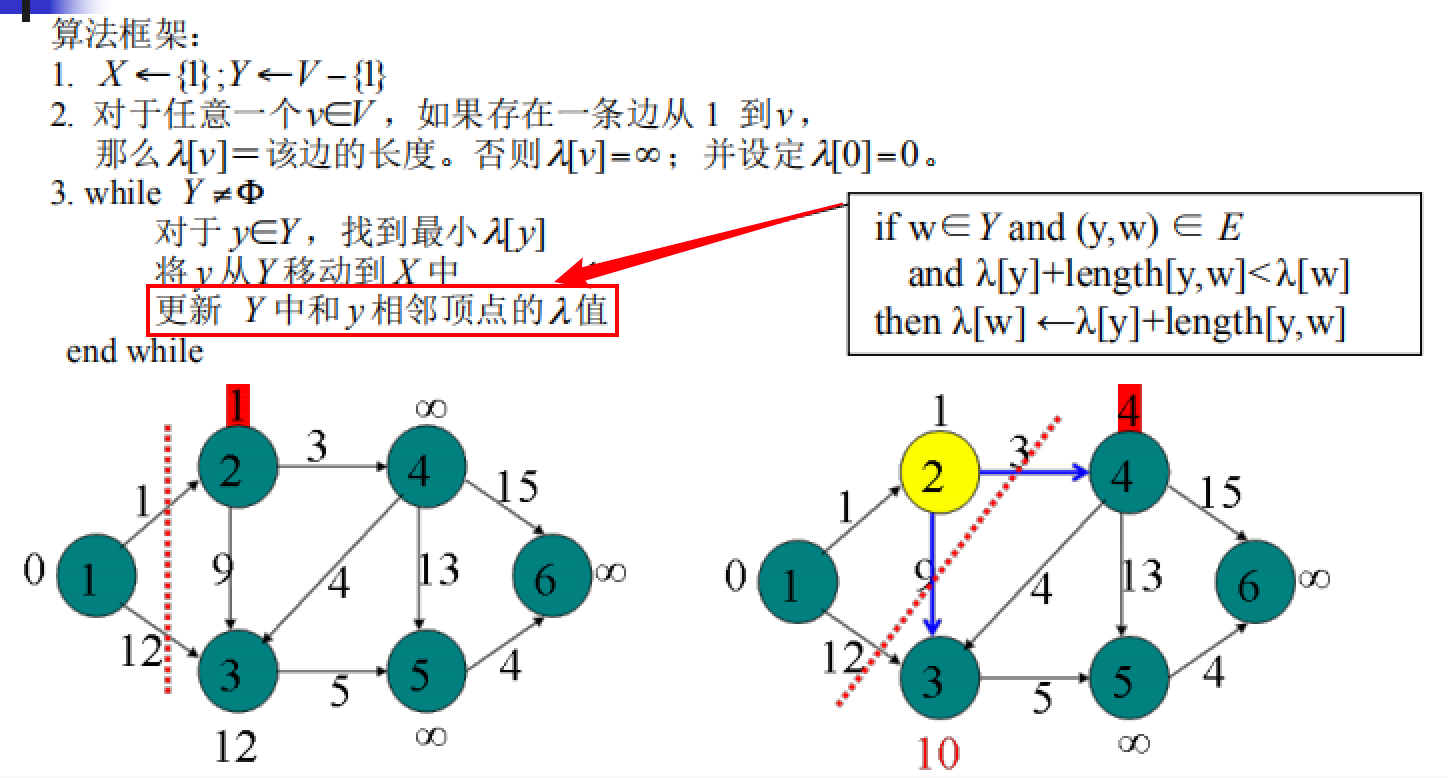
Dijkstra​

给定带权有向图 G =(V,E)，其中每条边的权是非负实数。另外，还给定 V 中的一个顶点，称为源。

  • 单源最短路径：要计算从源到所有其他各顶点的各边权之和的最短长度

image-20240603153832024

最小生成树​

设 G=(V, E) 是连通无向带权图，V = {1, 2,..., n}，即一个网络。E 中每条边 (v, w) 的权位 c[v][w]。

  • 生成树：如果 G 的子图 G' 是一颗包含 G 的所有顶点的树，则称 G' 为 G 的生成树。

  • 最小生成树：生成树上各边权的总和称为该生成树的耗费。在 G 的所有生成树中，耗费最小的生成树称为 G 的最小生成树。

构造 G 的最小生成树算法：

  • Prim 避圈法
  • Kruskai 破圈法

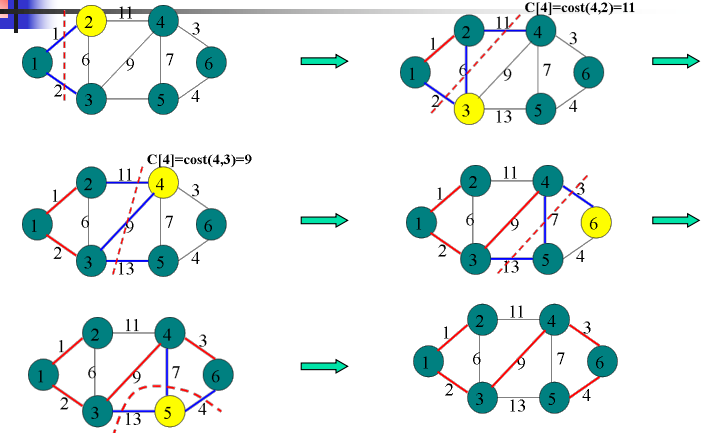
Prim 避圈法​

  1. 首先初始化构造集 X={1}

  2. 然后，只要 X 是 V 的真子集，就作如下的贪心选择选取权重最小的边 (x,y),其中x ∈ X，y ∈ Y，

    • 将边 (x,y) 加入当前的最小生成树，

    • 将顶点 y 从 Y 移到 X 中，

  3. 这个过程一直进行到构造集 X=V 时为止。在这个过程中选取到的所有边恰好构成 G 的一棵最小生成树。

image-20240524031646784

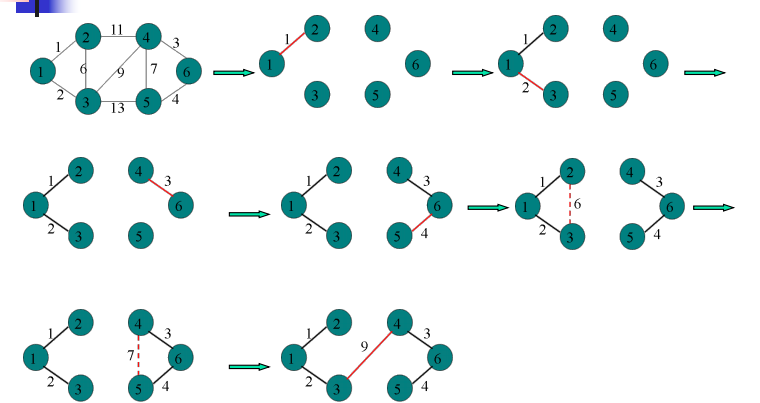
Kruskai 破圈法​

  1. 对 G 的边 E 按权重以非降序排列
  2. 初始时输出树 T={} 依次取排序表中的每条边，若加入 T 不形成回路，则加入 T 否则将其丢弃;
  3. 不断重复步骤 2，直到树 T 包含 n-1 条边（即 n 个节点），算法结束。

image-20240524031836951

Reference​

  1. My Chinese Blog