排序 Sort

Idea

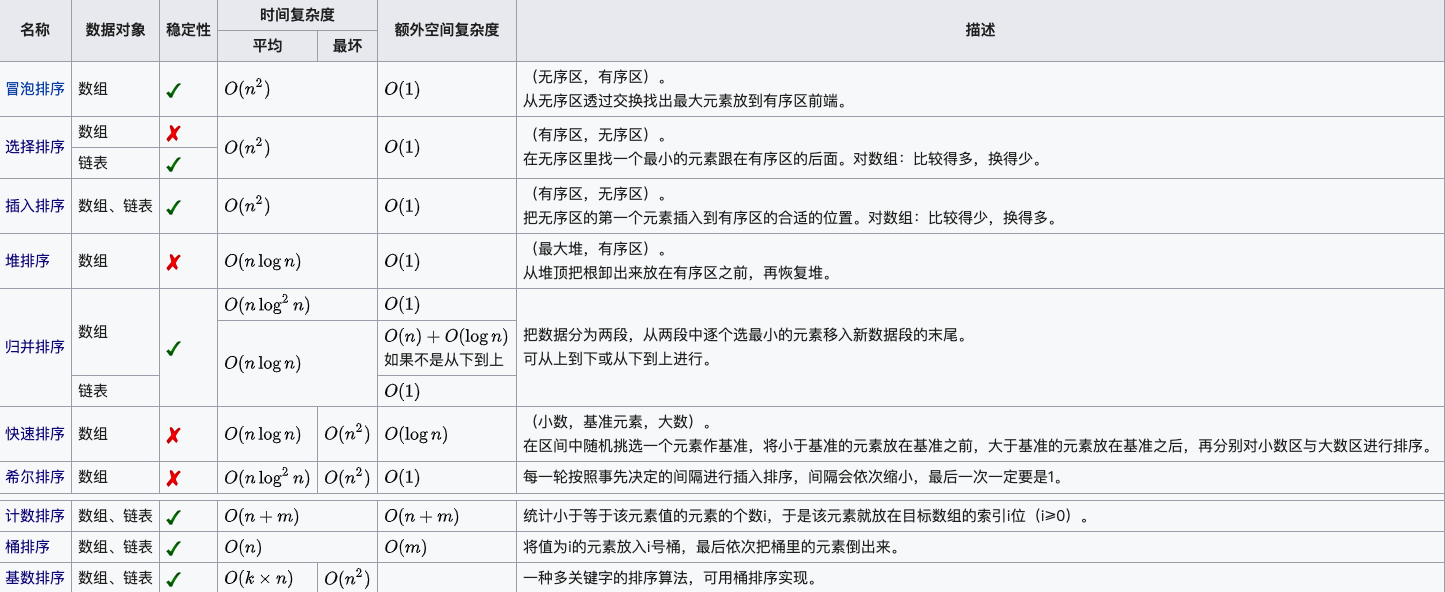
912. Sort an Array

Bubble Sort

Algorithm

• Find biggest element from unsorted area and put it into the sorted area.

Time Complexity: O(n^2)

Space Complexity: O(1)

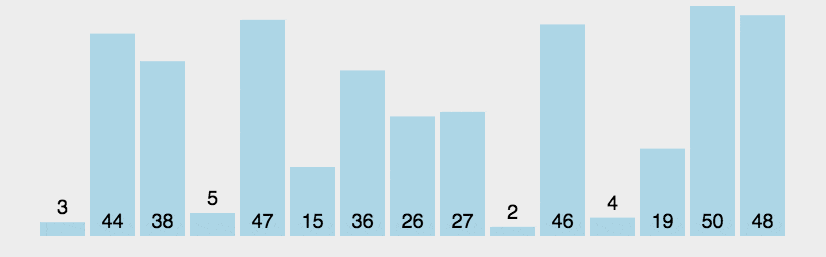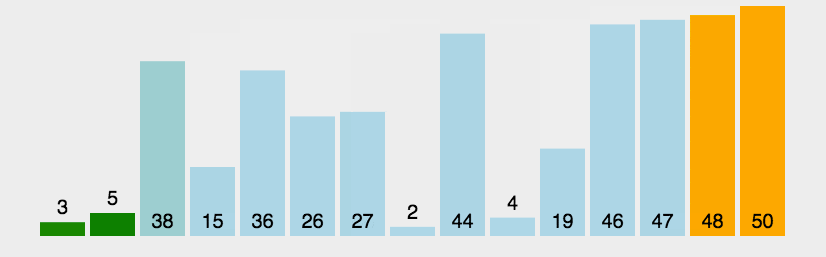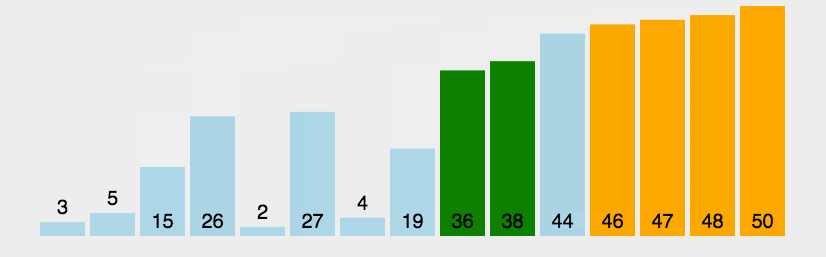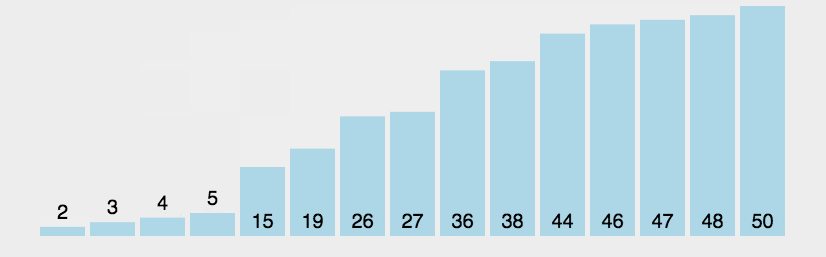
def bubbleSort(arr):
    for i in range(1, len(arr)):
        for j in range(0, len(arr)-i):
            if arr[j] > arr[j+1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr

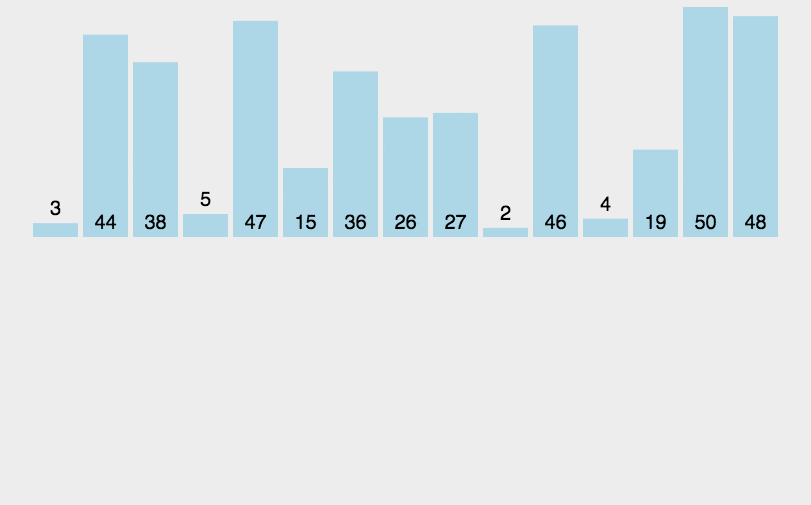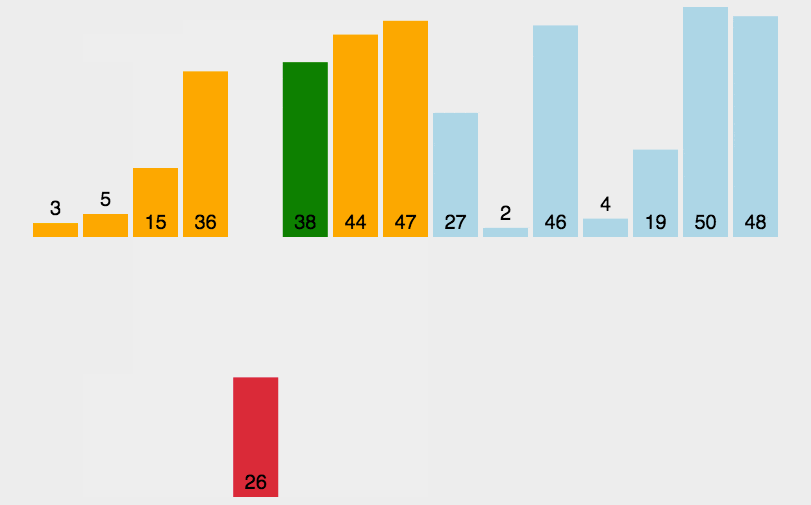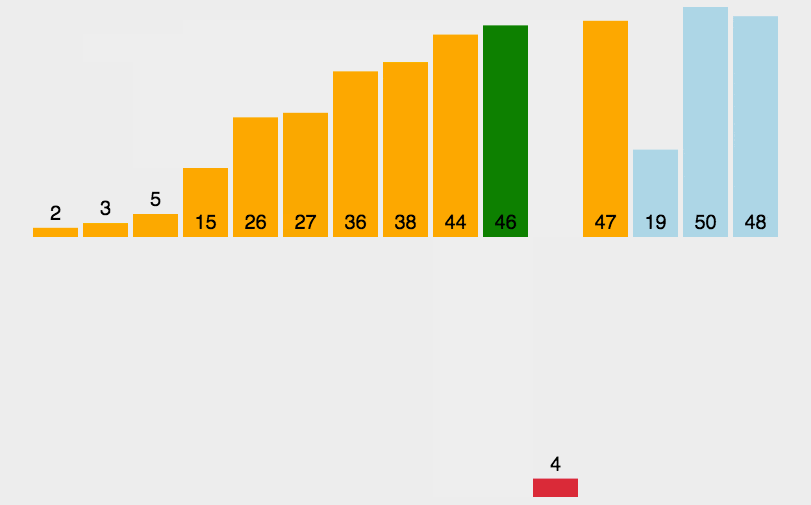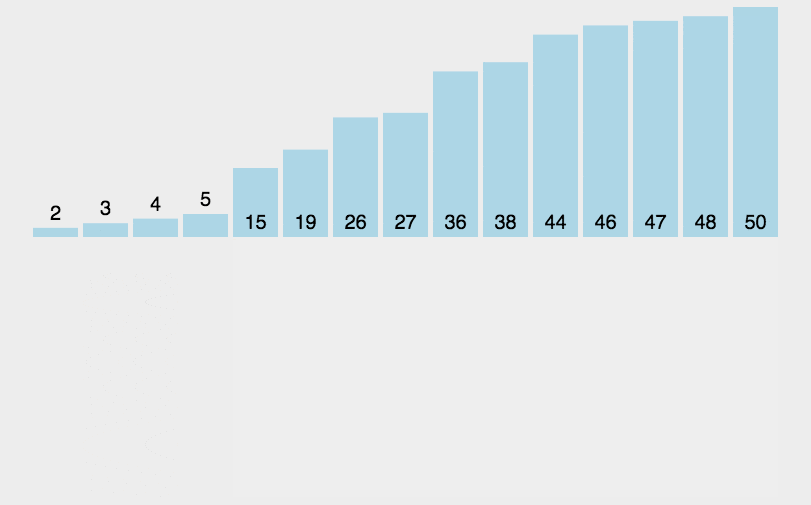
Insert Sort

Algorithm

• Split the array into sorted and unsorted subarrays
• Put the first unsorted element into the sorted Array
• Repeat above steps

Time Complexity: O(n^2)

Space Complexity: O(1)

def insertionSort(arr):
    for i in range(len(arr)):
        preIndex = i-1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex+1] = arr[preIndex]
            preIndex-=1
        arr[preIndex+1] = current
    return arr

Merge Sort

Algorithm

1. Split the array into two subarrays:

   1. Recurse processing subarrays

2. Merge the responding left array and right array

Time Complexity: O(nlogn)

Space Complexity: O(n)

def mergeSort(arr):
    import math
    if(len(arr)<2):
        return arr
    middle = math.floor(len(arr)/2)
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0))
    while right:
        result.append(right.pop(0));
    return result

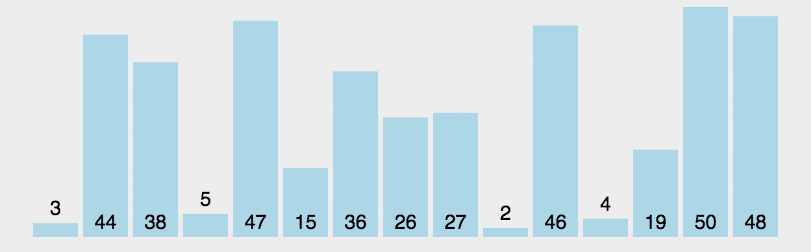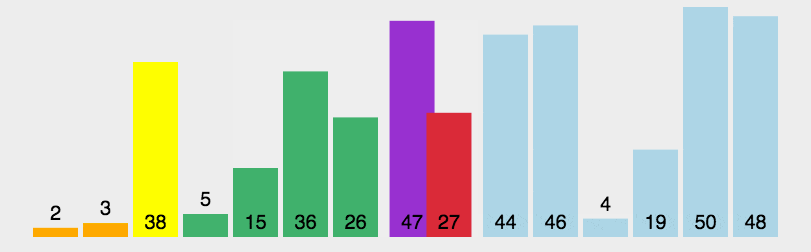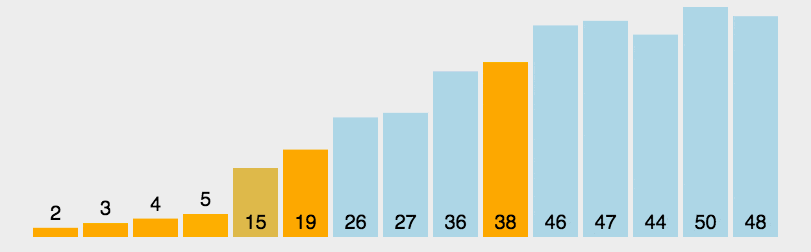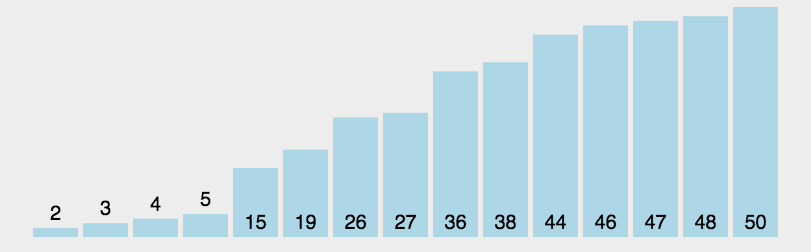
Quick Sort

Algorithm

1. Randomly find an element as the baseline
2. Split the array into two subarrays:
   1. Subarray with elements less than or euqal to baseline
   2. Subarray with elements larger than baseline
3. Recurse above steps until cannot split

Time Complexity: O(n^2)

Space Complexity: O(1)

def quickSort(arr, left=None, right=None):
    left = 0 if not isinstance(left,(int, float)) else left
    right = len(arr)-1 if not isinstance(right,(int, float)) else right
    if left < right:
        partitionIndex = partition(arr, left, right)
        quickSort(arr, left, partitionIndex-1)
        quickSort(arr, partitionIndex+1, right)
    return arr

def partition(arr, left, right):
    pivot = left
    index = pivot+1
    i = index
    while  i <= right:
        if arr[i] < arr[pivot]:
            swap(arr, i, index)
            index+=1
        i+=1
    swap(arr,pivot,index-1)
    return index-1

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]

Reference

1. My Chinese Blog
2. Merge Sort