Skip to main content

RNN Recurrent Neural Network

如果说卷积神经网络可以有效地处理空间信息， 那么循环神经网络（recurrent neural network，RNN）则可以更好地处理序列信息。

  • 通过引入状态变量存储过去的信息和当前的输入，从而可以确定当前的输出。

  • 许多使用循环网络的例子都是基于文本数据的

要点

  1. 序列模型
  2. 文本预处理
  3. 语言模型和数据集
  4. 循环神经网络
  5. 代码实现
  6. 通过时间反向传播

序列模型​

以股票价格（富时100指数）为例

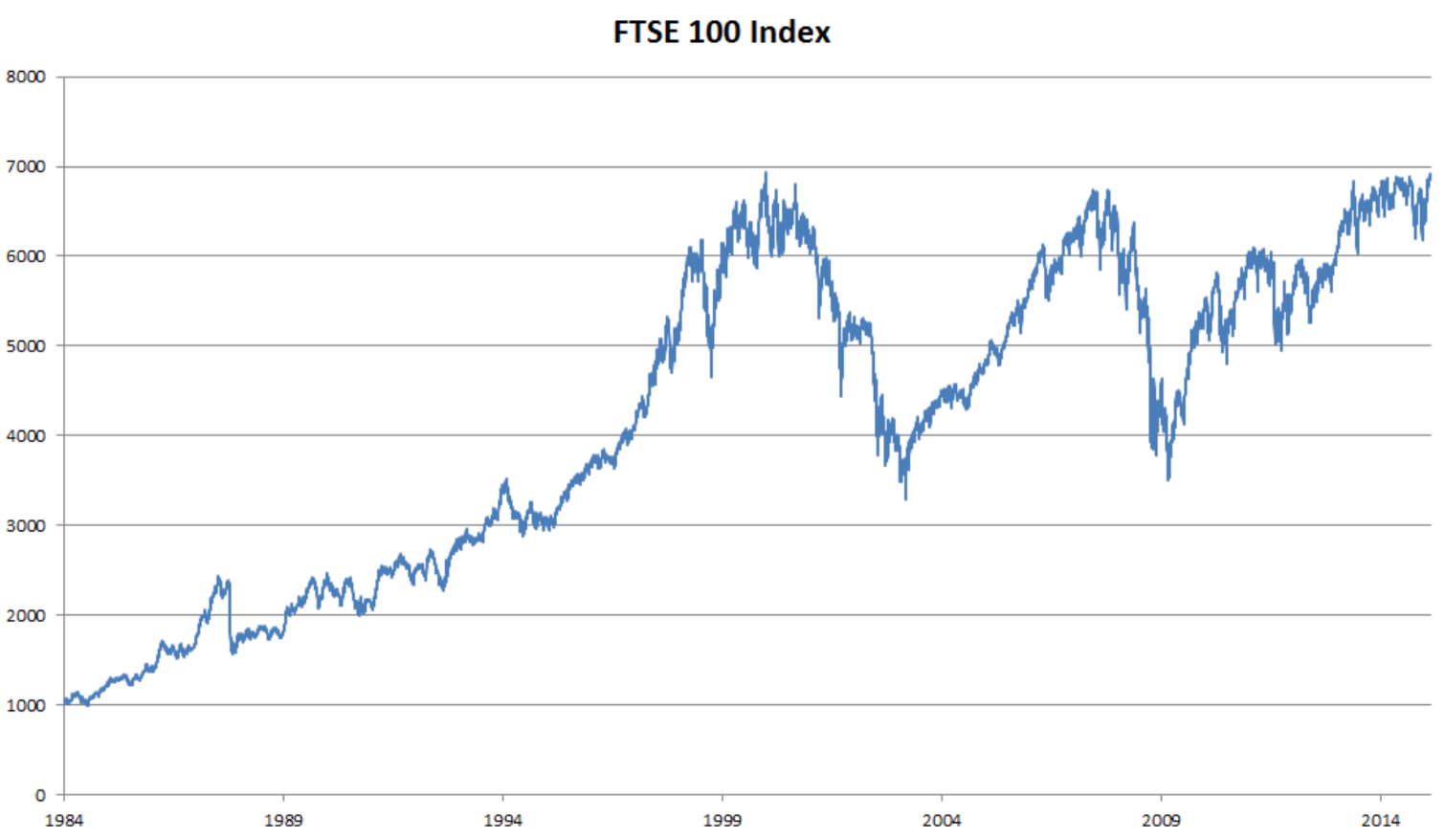
image-20240924101337467

设 xt 表示在时间点 t 的价格，我们想通过 xt−1,…,x1 来预测 xt。

image-20240924101317756

要点

  1. 马尔科夫模型，有限的X
  2. 引入隐变量h，训练两个函数

自回归模型​

可以使用回归模型实现这个预测。输入数据的数量， 输入 xt−1,…,x1 本身因 t 而异。有以下两种策略

  1. 我们可以使用长度为 τ 的 xt-1,…,xt-τ 的序列来预测 xt。
    • 因为是对自己执行回归，所以称为自回归模型（autoregressive models），
    • 优点：参数量是固定的
  2. 保留一些对过去观测的总结 ht 并同时更新预测 x^t 和总结 ht
    • 生成 ht=g(ht-1,xt-1)，再根据 xt=P(xt|ht) 估计 xt
    • 由于 ht 从未被观测到，所以称为隐变量自回归模型（latent autoregressive models）

image-20240924103006927

隐变量自回归模型公式如下

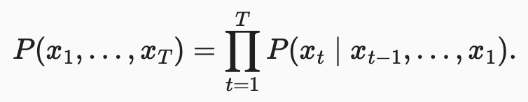
image-20240924103157232

tips: 如果要预测的是离散的单词，而不是连续的数字，可以使用分类模型而不是回归模型来估计 P(xt|xt-1,…,x1)

马尔可夫模型 Markov​

自回归模型使用 xt−1,…,xt−τ 而不是 xt−1,…,x1 来估计 xt，只要其是近似精确的，可以说序列满足马尔可夫条件（Markov condition）。

如果 τ=1，可以得到一个一阶马尔可夫模型（first-order Markov model），P(x) 公式如下。

  • 其表示产生 p(x1,...,xt) 序列的概率为 P(x1)*P(x2|x1)*...*P*(xt|wt-1)

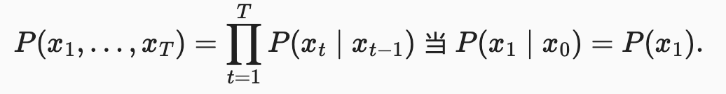
image-20240924103723978

而当 xt 为离散值时，可以得到下面公式，即预测 xt+1 只需要 xt 而不需要 xt-1

下面的公式推导请参考马尔可夫链的动态规划

image-20240924104820487

因果关系​

可以将 P(x1,…,xT) 倒序展开，基于条件概率有以下公式

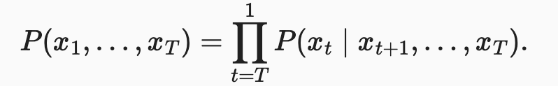
image-20240924105034312

如果基于一个马尔可夫模型， 我们还可以得到一个反向的条件概率分布。但很多情况下未来的事件不能影响过去，如何预测 P(xt|xt+1) 是一个研究方向。

训练​

我们可以使用正弦函数加上一些噪音来生成训练数据序列

将序列转换为模型的特征－标签（feature-label）对。 基于嵌入维度 τ ，将数据映射为数据对 yt=xt 和 xt=[xt−τ,…,xt−1] 。

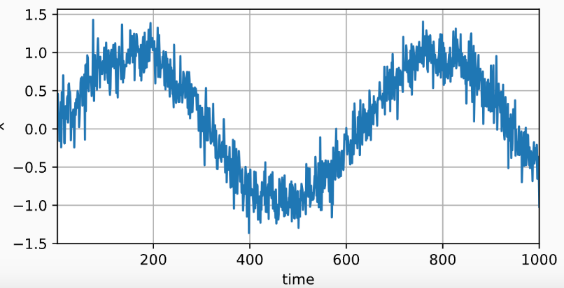
image-20240924143940662

在本次训练实验中

  1. 选用 MLP（具有一个隐藏层、一个ReLU激活层和一个全连接输出层） 来对预测数据进行训练。
  2. tau 为 4，选取的 [xt−τ,…,xt−1] 训练数据长度 n_train 为600，所以实际上选取的数据为 x1~x604

预测​

单步预测是基于原始数据预测，k步预测基于预测数据（而不是原始数据）来进行预测。

  • 模型预测下一个时间步的能力， 也就是单步预测（one-step-ahead prediction）
  • 对于直到 xt 的观测序列，其在时间步 t+k 处的预测输出 xt+k 称为 k 步预测（k-step-ahead-prediction）。
    • 利用以上的假设，tau 为 4，选取的 [xt−τ,…,xt−1] 训练数据长度 n_train 为600，所以实际上选取的原始数据为 x1~x604
    • 通过生成的预测数据 x601,x602,x603,x604 预测数据 x605，即为 1 步预测。
    • 通过生成的预测数据 x602,x603,x604,x605 预测数据 x606，即为 2 步预测，因为 x604 是最后的原始数据，k=606-604=2
    • 依此类推

tips: 这里看 d2l 书，特别不理解，花了很长时间才明白，这是因为书里

  • 单步预测使用了不止 x604 的数据
  • 而 multisteps 预测图中实际上是使用了截止至 604 的数据， k 值 越来越大
  • 而下面图例的 k=1,4,16,64 则是固定了某个 k 值

k=1, 4, 16, 64 的预测数据如下图，随着预测时间 k 值的增加，会造成误差的快速累积和预测质量的极速下降。

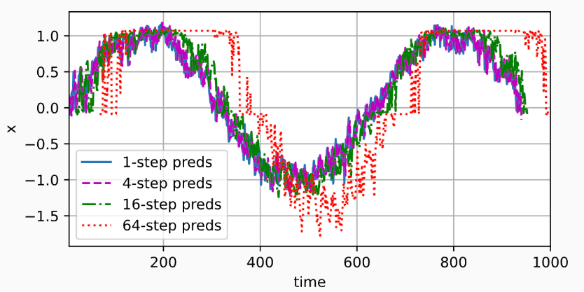
image-20240924145855237

文本预处理​

词元：。 每个文本序列又被拆分成一个词元列表，词元（token）是文本的基本单位。 最后，返回一个由词元列表组成的列表，其中的每个词元都是一个字符串（string）。

词表（vocabulary）：词元的类型是字符串，而模型需要的输入是数字，因此这种类型不方便模型使用。 现在，让我们构建一个字典，通常也叫做词表（vocabulary）， 用来将字符串类型的词元映射到从0开始的数字索引中。 我

将训练集中的所有文档合并在一起，对它们的唯一词元进行统计， 得到的统计结果称之为语料（corpus）。

语料库中不存在或已删除的任何词元都将映射到一个特定的未知词元。。。

语言模型​

语言模型给定X1,...,Xt，目标是估计文本序列联合概率

  • 预训练模型（BERT，GPT-3）
  • 生成文本
  • 判断序列是否常见

使用计数来建模 N元语法（N-gram）

使用马尔科夫假设

  • 一元语法：朴素贝叶斯假设，即tau为0
  • 二元语法：后一个元素只依赖于前一个，即tau为1
  • 三元语法：后一个元素依赖于前两个，即tau为2
  • ...
  • 七元语法有人搞过

计算复杂度非常关键，空间复杂度非常大

  • corpus 语料库
  • vocabs token index

image-20241002224714430

RNN 循环神经网络​

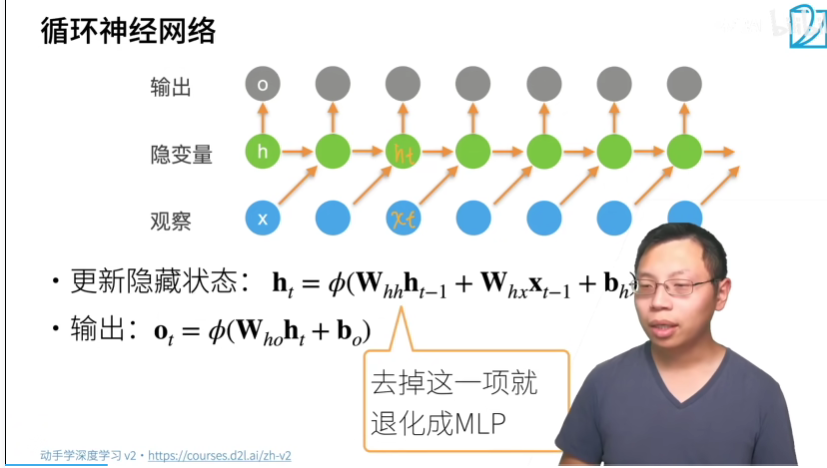
image-20240924003456850

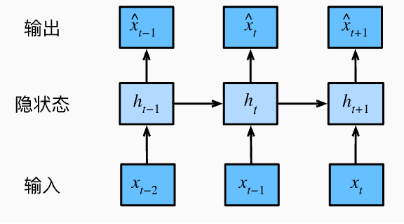
  1. Ht由Xt得到
  2. Ot由Ht得到
  3. Xt是Ot变化的根源，也是参数更新的根源
  4. Xt是Ht生成的根源

X的序列信息存在Whh参数里

因此这样的隐藏变量被称为隐状态（hidden state）。 由于在当前时间步中， 隐状态使用的定义与前一个时间步中使用的定义相同， 计算是循环的（recurrent），于是基于循环计算的隐状态神经网络被命名为循环神经网络（recurrent neural network）。 在循环神经网络中执行计算的层 称为循环层（recurrent layer）。

  • 在本例中，模型参数是Wxh和Whh的拼接， 以及bh的偏置，所有这些参数都来自 (8.4.5)。 当前时间步t的隐状态Ht 将参与计算下一时间步t+1的隐状态Ht+1。 而且Ht还将送入全连接输出层， 用于计算当前时间步t的输出Ot。
  • 隐状态中 XtWxh+Ht−1Whh的计算， 相当于Xt和Ht−1的拼接 与Wxh和Whh的拼接的矩阵乘法
  • 我们考虑使用 字符级语言模型（character-level language model）
  • 在实践中，我们使用的批量大小为n>1， 每个词元都由一个d维向量表示。 因此，在时间步t输入Xt将是一个n×d矩阵

评估：困惑度（Perplexity）

我们可以通过计算序列的似然概率来度量模型的质量。

损失函数，平均交叉熵

  • 如果想要压缩文本，我们可以根据当前词元集预测的下一个词元。 一个更好的语言模型应该能让我们更准确地预测下一个词元。 因此，它应该允许我们在压缩序列时花费更少的比特。 所以我们可以通过一个序列中所有的n个词元的交叉熵损失的平均值来衡量：

每次分类的交叉熵平均得到平均交叉熵

预测

这被称为预热（warm-up）期， 因为在此期间模型会自我更新（例如，更新隐状态）， 但不会进行预测。 预热期结束后，隐状态的值通常比刚开始的初始值更适合预测， 从而预测字符并输出它们。

梯度爆炸或梯度消失， 以及需要对循环神经网络分离梯度

其他​

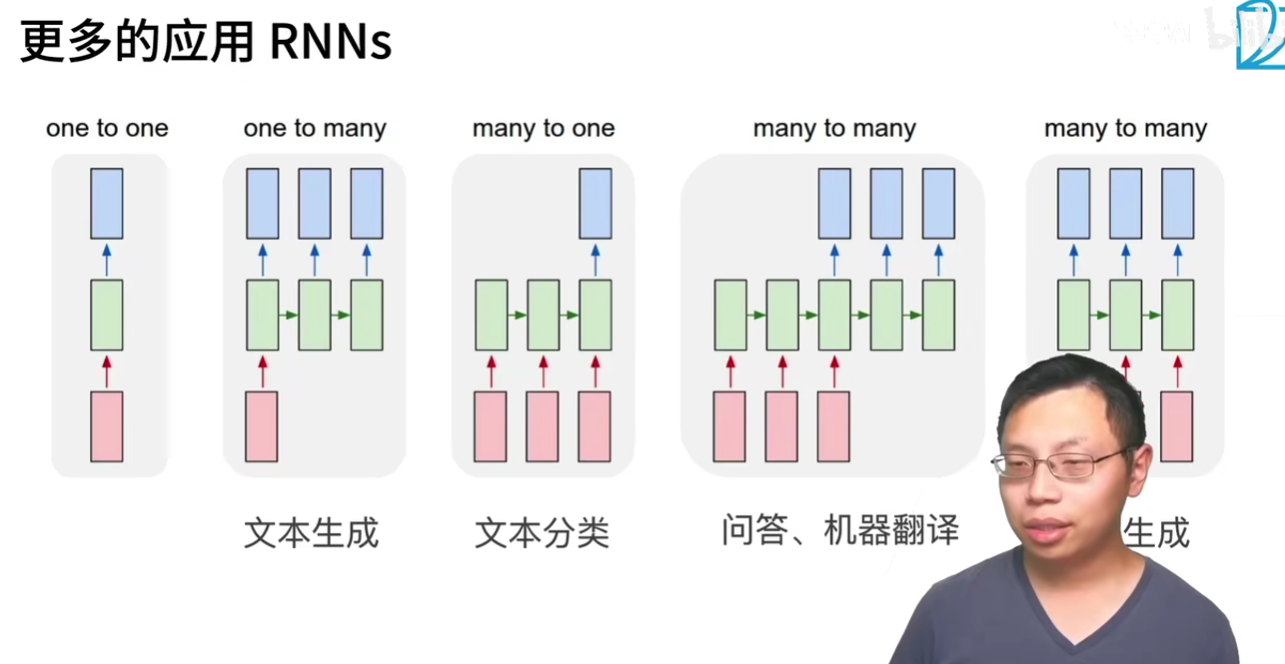
RNN 应用​

  1. 1 到多，文本生成
  2. 多到 1，文本分类
  3. 多到多，问答、机器翻译
  4. 多到多，其他的生成

image-20240924011947939