Skip to main content

Transformer Inference Arithmetic

截至 2022-03-30

这篇文章介绍了 Transformer 模型中推理参数量、延时的计算，没有复杂的数学推导，与实验效果类似，有助于对 Transformer 有深入的理解。

前置知识：

重新算一遍​

head_size x num_head = d_model

attention

  1. Model Weight(Wqkvz): 4 x d_model x head_size x num_head = 4 x d_model^2
  2. KV: 2 x batch_size x seq_len x d_model x head_size x num_head 这部分不算base model的参数量

FFN

  1. Model Weight: 8 x d_model^2

所以模型总参数量是 12 x d_model^2 x n_layers，即 12 x 8192^2 x 64 x 2 = 52e9

由于使用float16，所以模型总大小为 52e9 x 2 = 104e9 = 104GB

Flops

Attention

  1. KQVZ: 4 x 2 x d_model x head_size x num_head = 8 x d_model ^2

FFN

  1. 2 x 2 x 4 x d_model x d_model = 16 x d_model ^2

所以总的 flops 也是 24 x d_model^2 x n_layers

LLM Parameter Counting by kipply​

模型训练过程中的权重的参数都是半精度浮点数，通常是 2 bytes 因为目前大部分训练都是在 half-precision（bfloat，但不是所有的半精度都是 bfloat） 下进行的。2020 年 的 GPT-3 Paper 使用了 half-precision。

解码器由 self-attention 层与 FFN 层组成，权重大小如下

  1. self-attention 自注意力层
    1. Wq, Wk, Wv 权重矩阵，其尺寸为 (d_model, n_heads, d_head), 被用来把 input 映射成 QKV 向量
    2. Wo 权重矩阵，其尺寸为 (d_model, n_heads, d_head), 用于 self-attention 层的输出，接下来会传入 MLP 层（用于把拼接的 Z 映射为输出的 Z）
    3. 所以这层的权重大小为 3*(d_model*n_heads*d_head)+d_model*n_heads*d_head=3*d_model*n_model+d_model*n_model=4*d_model^2
    4. 实践中（Attention Is All You Need），d_model （也即 d_embedding 的尺寸）为 512，n_deads 为 8，d_head 为 64（在大多数 Transformer 架构中，d_head*n_head=d_model，d_head 也称为 Key/Value Size）
  2. MLP 多层感知机，也称为 Linear Layer 线性层，FFN Layer 前向反馈层
    1. 这部分有两个全连接层，第一层大小为 d_model*(4*d_model)=d_model^2*4， 第二层大小为 (4*n*d_model)*d_model=d_model^2*4，
    2. 所以这层的权重是两个 d_model^2*4 矩阵，总大小为 d_model^2*8 ⭐️
    3. 实践中，MLP 层的隐藏层大小是 d_model 的 4 倍，即 512*4=2048。每层都有一个偏置向量（此处不表），第一层偏置向量的大小为 4*d_model，第二层偏置向量的大小为 d_model，总计为 5*d_model
  3. Layer Normalization 层（此处不表），大小为 d_model
    1. 归一化权重（Layer Norm Weights）：用于层归一化的缩放参数。
    2. 归一化偏置（Layer Norm Biases）：用于层归一化的偏移参数。

在忽略偏置向量权重的情况下，可以计算模型的总权重如公式所示，

  • 4*d_model^2+8*d_model^2=12*d_model^2
    • n_layers 为 64，是编码器堆叠层数
    • d_model（input_embedding）大小为 128*n_layers=8192
    • 计算得到 52B 模型的参数量

image-20241001113044239

这里的52B指的是52Billion个参数，不是52B个byte，总大小应该是52Billion bytes

以上的计算还忽略了 Layer Normalization d_model 的参数，MLP 的偏置参数，以及位置编码的参数（在 GPT2 和原始 Transformer 中为 n_ctx+d_model，在Gopher 280B 模型中，有 21.5B 个参数用于相对位置编码），但在 Kipply 作者的表述中，这些参数量都可以忽略不计（zero）。

by ChatGPT​

在一个深度学习模型中，特别是像GPT这样的变压器模型，每个“块”通常包含以下组件。每个块（或层）通常包括一个自注意力层和一个前馈神经网络层。以下是每个块中的主要权重和参数：

  1. 自注意力层（Self-Attention Layer）

    • 查询权重（Query Weights）：用于生成查询向量的权重矩阵。

    • 键权重（Key Weights）：用于生成键向量的权重矩阵。

    • 值权重（Value Weights）：用于生成值向量的权重矩阵。

    • 输出权重（Output Weights）：用于将注意力机制的输出映射回原始维度的权重矩阵。

  2. 前馈神经网络层（Feedforward Layer）

    • 第一层权重（Feedforward Layer 1 Weights）：用于第一个线性变换的权重矩阵。

    • 第一层偏置（Feedforward Layer 1 Biases）：用于第一个线性变换的偏置向量。

    • 第二层权重（Feedforward Layer 2 Weights）：用于第二个线性变换的权重矩阵。

    • 第二层偏置（Feedforward Layer 2 Biases）：用于第二个线性变换的偏置向量。

  3. 层归一化（Layer Normalization）

    • 归一化权重（Layer Norm Weights）：用于层归一化的缩放参数。

    • 归一化偏置（Layer Norm Biases）：用于层归一化的偏移参数。

这些权重和参数在训练过程中通过反向传播算法进行调整，以最小化损失函数，从而使模型能够有效地执行其任务。

Arithmetic​

  • KV Cache 解释了缓存 Self-attention 向量带来的性能提升，带来的权衡（tradeoffs）和成本。
  • Capacity 介绍了 KV Cache 的存储成本，把它与模型权重存储联系起来，讨论 capacity 对性能的影响
  • Model Parallelism 介绍了张量并行以及通信成本
  • Latency Calculations 推理延时的计算 create equations that serve as floorlines for inference speed
  • batch size 介绍 batch size 对性能的影响，以及最佳的 batch size
  • flops counitng 讲解了在 transformer 模型中每个块的 flops 计算速度，可以看出哪个块是计算密集型
  • Intermediate memory costs 介绍了激活层需要额外的内存，以及在真实的基准（beachmarks）上内存带宽消耗是多少
  • comparing against real benchmarks 和 Nvidia 的 FasterTransformer benchmarks report 作比较，明确差异在哪里

KV Cache​

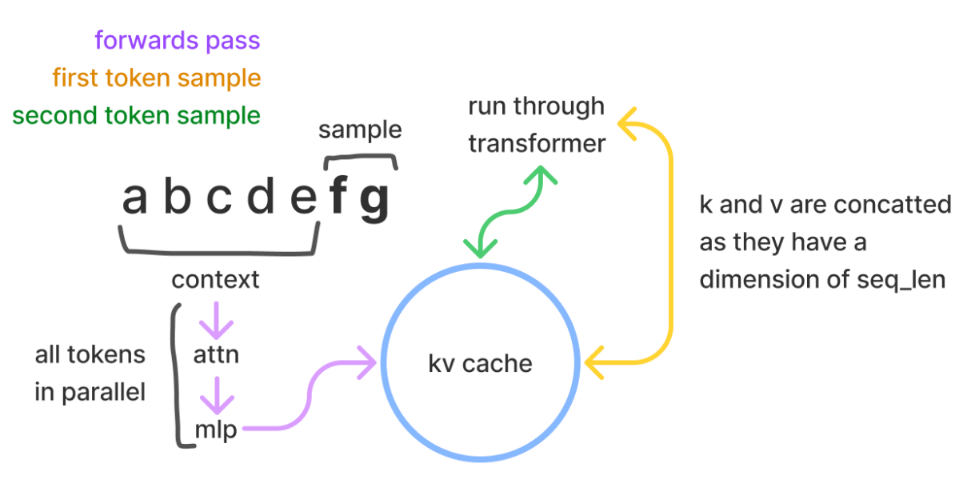
Transformer 推理主要包括两个步骤：首先并行处理提供的prompt，然后逐个生成新的 token（这就是自回归性质的体现）。

如下所示，在推理过程中，每个 token 都需要获取历史序列中每个 token 的键值对（kv）向量来计算自注意力（如下图所示，q1需要与k1v1，k2v2等计算得到z），无论这些 token 是来自初始的提示/上下文，还是生成的 token。这些键值对可以存储在一个被称为 kv 缓存（或称为过去缓存）的矩阵中。

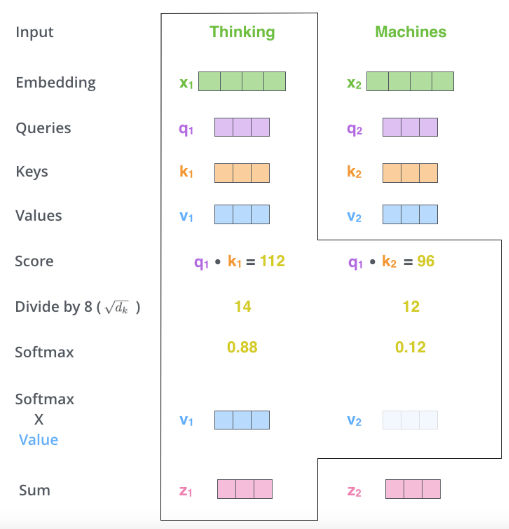
image-20241003005424490

KV Cache需要的维度为 [batch, 2, num_heads, seq_len, features]。（没有head_size嘛？）

  • batch 是批次大小
  • 2 表示的是 key（键）和 value（值）两个矩阵，每个 token 都有一个 key 和一个 value
  • num_heads 是多头注意力数量
  • seq_len 是输入的序列长度
  • features 是 token 的大小

image-20241003005813311

一个token的KV存储​

KV cache 的目的是避免对一个 token 的重复计算，因为参数是固定的，一个 token sampling 得到的 KV 向量也是固定的。我们可以把 KV 向量缓存起来，以空间换时间。其中，对于每个 token，我们需要的存储空间的大小如下（单位为 bytes）

image-20241003010126543

  • 第一个 2 代表 K，V 两个向量
  • 第二个 2 是存储单位的大小，此文中我们使用 float16，有 2 个 bytes
  • 接下来是 n_layers x n_heads x d_head，分别是解码器堆叠数 n_layer，n_heads 注意力头数，d_head 每个头的输出大小

一个token的KV计算flops​

一个 token 的 KV 向量的计算 flops（每秒浮点运算操作）如下所示

image-20241003010659715

  • 第一个 2 代表 K，V 两个向量
  • 第二个 2 与 d_model^2 是矩阵乘带来的
  • n_layers 是解码器的堆叠数

在一个矩阵乘（matmuls，matrix multiplication）中有多少浮点计算次数 flops（Floating-point operations per second）？

  1. 在 w(m, n) 与 x(n, 1) 的矩阵乘 wx(m, 1) 中，有 2mn 次运算。其中第一个 2 是因为矩阵乘 matmuls 需要计算（1）乘法（2）加法，即乘法后的累加。

  2. 在 w(m, n) 与 x(n, p) 的矩阵乘 wx(m, p) 中，有 2mnp 次运算

通过上述 Flops 计算公式可得，在 52B 参数的模型中（以 Anthropic's 为例 d_model 为 2^13=8192，n_layers 为 64），总 flops 如下

image-20241003012159648

flops bound VS memory bound（一个token的计算和内存加载时间）​

A100 每秒可以执行 312e12 次 flops 操作（312TFLOPS），内存带宽为每秒 1.5e12 bytes，比值为 312/1.5=208。

所以模型所需的存储和计算时间如下

image-20241003012430501

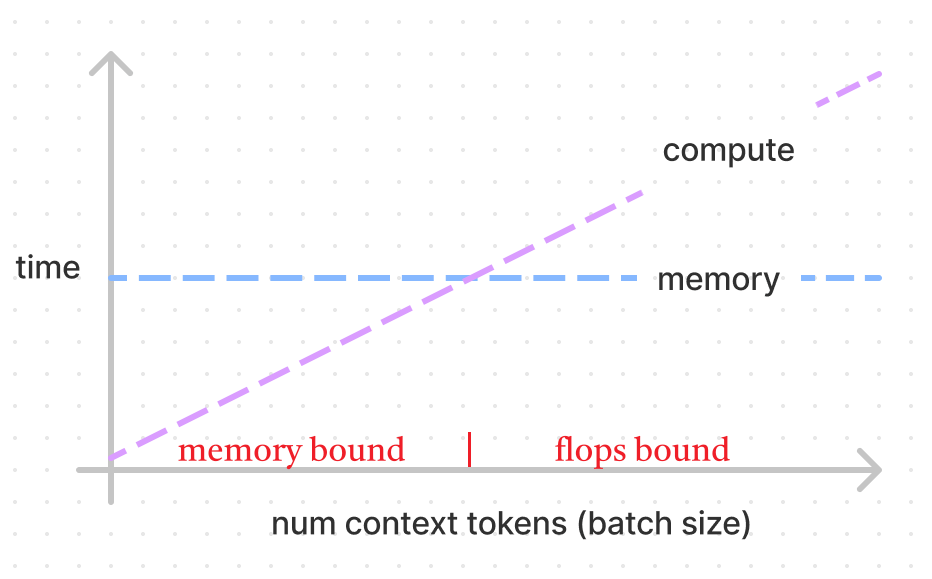
下图展示了计算与内存加载时间的关系，batch size 越大计算时间越多，而内存加载时间不变。对于 A100 而言，两线交点为 208 （ops:bytes），计算速度是内存加载速度的208倍。Nvidia 将计算时间与内存加载时间的对比称为“数学带宽”（math bandwidth），来形容这个受限关系。

  • 如果少于 208 ，内存加载时间大于计算时间，为 memory bound（内存受限）。意味着处理器在等待内存传输完成，加载速度跟不上计算速度，内存带宽达到瓶颈。
  • 如果超过 208，计算时间大于内存加载时间，为 flops bound（flops受限）。意味着计算能力达到瓶颈，内存带宽不是限制因素。

image-20241004031028247

其他​

  • 对于 52B 的模型而言，前向计算 208 个 tokens 所需的权重加载时间为 2*12*n_layers*d_model^2/1.5e12~=69 millisecs ，如果使用 4 个并行的 GPU，则约为 17 毫秒，如果有 416 个 tokens，会花两倍的时间，312 个 tokens 则需要 1.5 倍的时间。

  • 计算一个 KV cache token 的时间（2*2*n_layers*d_model^2）是一次前向计算的时间（2*4*n_layers*d_model^2）的1/6，一般来说prefill并行前向计算都非常快，而 sampling（decode） 则需要获得每个历史 token 的 KV 来计算自注意力。

    • 但实际上，每一步推理，都省了前面所有tokens的KV计算时间 n_tokens * 2*2*n_layers*d_modes，所以没有KV Cache的时候，decode阶段的时间复杂度将变成 O(n^2)

  • 有时，小 batch 会造成 memory bound 而不是 flops bound，这时我们更愿意去重新计算 KV 而非用过去的 cache。(我认为仅在小batch的情况下)

52B 模型参数维度​

Anthropic's 提及的 52B 模型

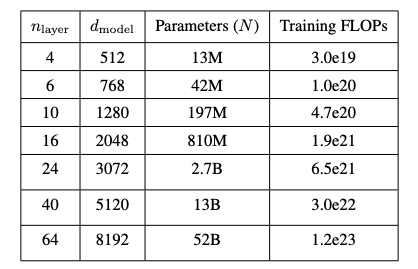
image-20241004032513622

  • n_layers 为 64
  • n_heads 为 128
  • d_head 为 64
  • d_model 为 128*n_layer = 8192
  • n_voc 为 2^16

image-20241004032517358

Nvidia A100 性能指标​

  1. flops 312e12

  2. 内存带宽 1.5e12 bytes

  3. flops/内存带宽= 312/1.5= 208，对于其他GPU不一样

  4. 显存大小 40GB

  5. 通信带宽 300GB/s

KV 缓存 Capacity​

在 GPU 中存储两个东西：KV Cache 和 Weights。

以 Nvidia A100 GPU 为例，其有 40GB 显存。

52B模型参数大小​

52B 模型的参数存储空间如下所示，乘以2是因为 float16 有 2bytes

  • 此处52B的参数量是 52e9

image-20241004024854938

一个 A100 显存有限，考虑放在多个 GPU 中，三个 A100 共 120GB，去掉 104GB 模型参数，还剩 16GB 用来做 KV Cache。

16GB能装下 8000 个 tokens​

  • n_layers 为 64
  • n_heads 为 128
  • d_head 为 64

image-20241004024941777

所以上面剩下的 16GB 只能装下 16/0.002≈8000 tokens，可以设置大小为 4 的 batch size，每个 batch request 可以处理最多 2048 个 tokens。

batch size 与 memory bound​

我们希望 batch size 能够大一些（提高一次推理中的处理的请求量），这样子能够多利用内存带宽，提高计算量，处理更多请求。

如果 batch size 太小的话，我们会陷入 memory bound，即内存带宽没有跑满（因为加载1个token和加载208个token的时间是一样的），计算量并不饱和，可以考虑舍弃 KV Cache，直接进行计算。可以考虑新增一个 GPU，组成 4 个 GPU 增大显存总额，有更多空间做 KV Cache，从而能够增大 batch size。

  • TODO：为什么这里不是 4 个 batch，2000 个 tokens？
    • => GPT：选择 2048 而不是 2000，主要是因为 2048 是 2 的幂次方，而计算机系统（尤其是 GPU）在处理二进制数据时，对于这些特定的数字往往更高效。不用非常严谨.

在中间的计算步骤中也有一些存储的需求，但他们可以忽略不计。

模型并行 Model Parallelism​

下面描述一个模型并行的实现，以便对齐进行性能评估以及计算通信损失。

模型并行会带来一个问题，即内存加载权重的成本与计算量 flops 都会被拆分到每个GPU中。每个GPU都会使用其部分权重计算，并且在需要同步时通信。而在流水线并行中，每个 GPU 都会分配到一部分的权重。

  • 在训练时，GPU可以一个接一个处理多个 batch 的数据，但在推理时，请求量小的情况下GPU会闲置下来。
  • 在流水线并行中，常常会遇到 flops bound，内存带宽并不会用满。
  • 唯一比模型并行好的是通信开销不同，流水线并行的通信开销为 d_model，而模型并行的通信开销是 N*d_model，此处的 N 是 GPU 的数量。

A100 的通信带宽是 300GB/s

  • TODO: The doc marks it as 600GB/s because Nvidia is adding up 300GB/s into each chip and 300GB/s out simultaneously rather than using a bidirectional number (which will be more intuitive for our calculations). => bidirectional 是什么意思？

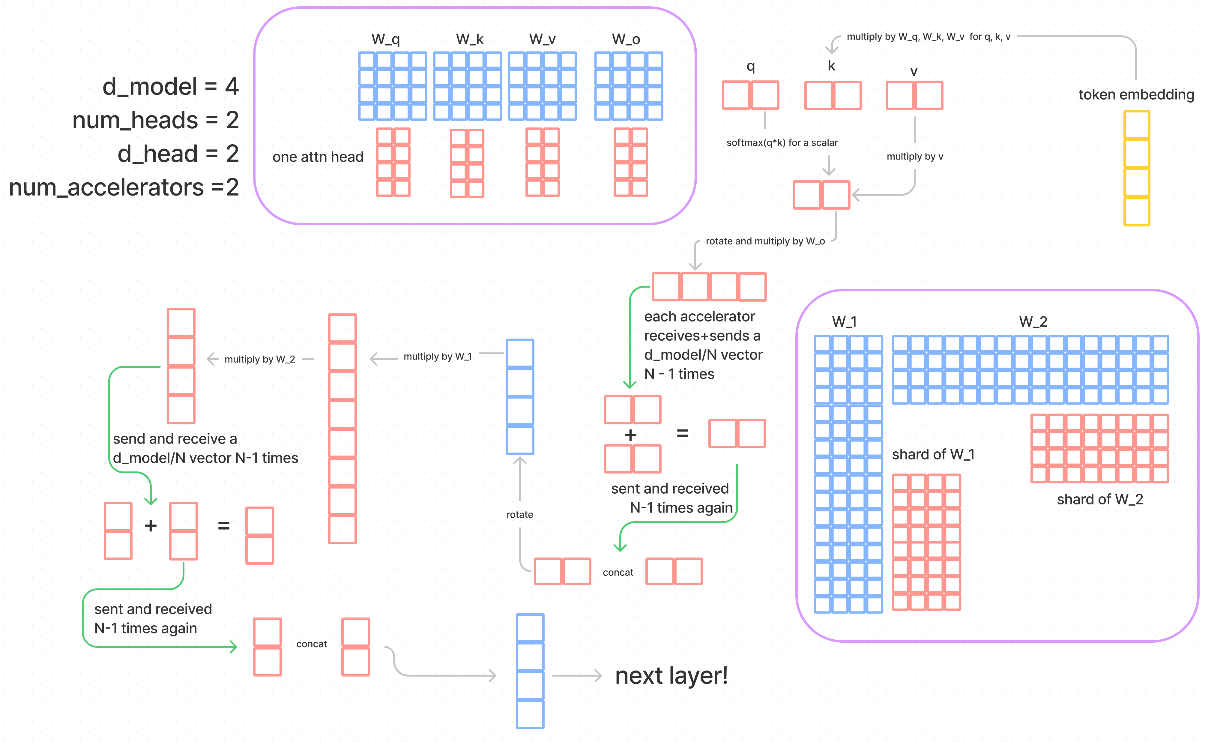
image-20241004040213934

上图表述中，模型并行的核心是按注意力头 head 来把参数（WQ, WK, WV, WO, W1, W2）划分到各个 GPU 中。

  • num_heads 为注意力头数量 2
  • num_accelerators 代表着 GPU 数量，此处为 2，与 num_heads 一致。在上图场景也称作 N
  • d_model 为 token embedding 大小 4
  • d_head 为注意力头大小 2

计算 flow 详解​

  1. 输入 X 大小（1,4）
  2. WQ, WK, WV 原来大小为 (4, 4)，按 num_heads 划分 sharding （2, 4）到每个 gpu 中
    1. 由于 Transformer 架构中，计算 Z 本身就是每个注意力头各自计算，最后拼接得到 Z，所以此处 Softmax(XWQ*WK)WV 得到的 Z 与未并行情况下的 Z 是一致的
  3. 对于一个 GPU 来说，乘以 WO 最终得到输出 Z 后，这个 Z 虽然尺寸与未 sharding 一致为（1,4），但每个元素的值都不完整。
    1. 未并行情况下，Z(1,4) x WO(4,4)。并行情况下 Z(1,2) x WO(2,4)，得到的输出都为（1,4）
    2. 假设 Z 矩阵称为 x，WO 称作 y。则原来的 Z11 = y1x11+y2x12+y3x13+y4x14。但在 GPU0 的 Z11 = y1x11 + y2x12，缺少的另外的y3x13+y4x14在GPU1中，所以我们需要把两个 GPU 的 Z11 相加才能得到和未并行情况一致的 Z。
  4. 综上所述，GPU0 有一个输出 Z(1,4)，GPU1 有一个输出 Z(1,4)，需要将他们矩阵加法才能得到正确的输出 Z
    1. 在这里的模型并行中，提到 GPU0 负责 Z[0, 1] 的加法，GPU1 负责 Z[2,3] 的加法，所以 GPU0 需要传输 Z[2,3] 给 GPU1，GPU1 需要传输 Z[0,1] 给 GPU0。这是上图提到的第一次 send and receive N-1 times
    2. 最终 GPU0 拥有正确的 Z[0, 1]，GPU1 拥有正确的 Z[2,3]，他们需要在做第二次传输，这是上图提到的第二次 send and receive N-1 times
    3. 最终 GPU0 将 Z[0,1] 与 Z[2,3] 拼接得到最终的输出 Z[0,3]，GPU1 也同理（此处每个 GPU 都需要得到最终的输出 Z 是因为接下来的 FFN 需要完整的 Z）
  5. 接下来的 FFN 层的 W1 W2 也是同理按 num_heads 划分都 GPU 中并行计算
    1. 分析与上面 WO 矩阵的并行分析一致
    2. 原来的自注意层输出的 Z(1,4)，W1(4,16), W2(16, 4)
    3. 按 nun_heads 划分后，每个GPU的W1(4,8), W2(8, 4)
    4. 假设 FFN 层输出为 Y，那么 Y11=W2_1,1(W1_1,1xZ_1,1+W1_2,1xZ_1,2+W1_3,1xZ_1,3+W1_4,1xZ_1,4) +...+ W2_16,1(W1_1,16xZ_1,1+W1_2,16xZ_1,2+W1_3,16xZ_13,+W1_4,16xZ_1,4)
    5. 模型并行后，GPU0 获得的 Y 尺寸为（1,4），但 Y11 = W2_1,1(W1_1,1xZ_1,1+W1_2,1xZ_1,2+W1_3,1xZ_1,3+W1_4,1xZ_1,4) +...+ W2_8,1(W1_1,8xZ_1,1+W1_2,8xZ_1,2+W1_3,8xZ_13,+W1_4,8xZ_1,4)
    6. 可以看出 GPU0 中的 Y11 也是不完整的，需要与 GPU1 做 N-1 次发送接收通信，相加后，再做 N-1 次发送接收通信
  6. 此处忽略 layer norm 层的计算
  7. 最终每个 GPU 都得到了一层的完整输出 X

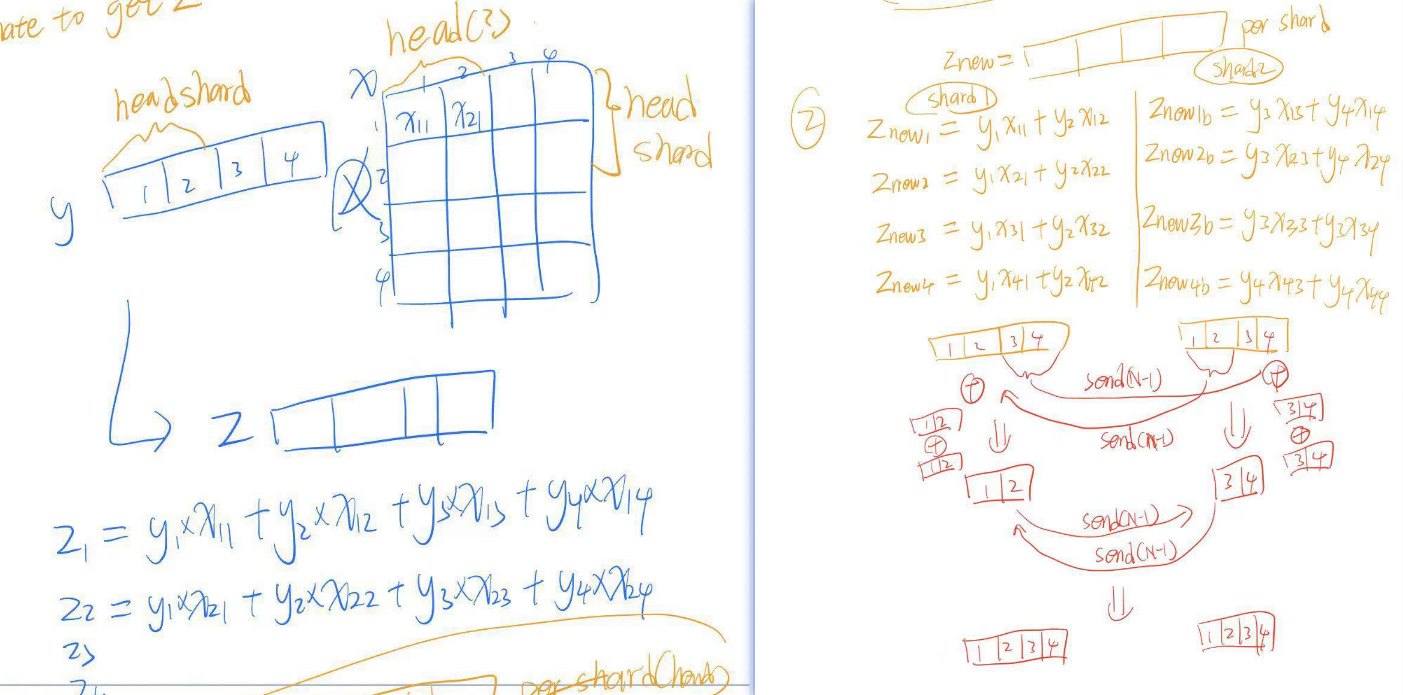
image-20241005024052855

泛化公式​

  1. 自注意层的 Wq, Wk, Wv 原始维度为 (d_model, d_head*num_heads)，如果模型并行到 N 个 GPU 上，他们的维度变为 (d_model, d_head*num_hdeas/N)
  2. FFN 层的 W1 原始维度 (d_model, 4*d_model)，并行到 N 个 GPU 上，维度变为(d_model, 4*d_model/N)
  3. FFN 层的 WW 原始维度 (4*d_model, d_model)，并行到 N 个 GPU 上，维度变为(4*d_model/N, d_model)
  4. 其中，总共进行了 4(N-1)d_model/N bytes 的通信
    1. TODO: 这里的通信 bytes 应该还需要再乘以 2？因为 d_model 是 float16，2bytes

延时的计算 Latency Calculations​

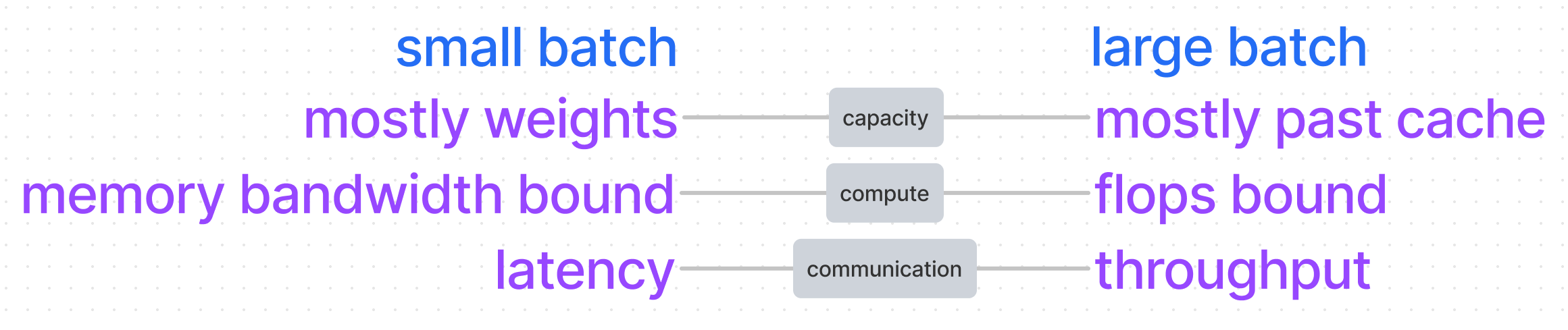
image-20241005023838929

批量大小对延时的影响​

如上图所示，要计算一个 token 的推理延时

  • 小批量时，内存中基本都是模型参数，主要是 memory bound，flops 计算资源充裕，对于通信延时而言，通信带宽也没有打满，可以直接估计为尽可能小的通信延时。
  • 大批量时，内存中基本是KV Cache，主要是 flops bound。对于通信延时而言，由于需求大，已经要考虑通信的吞吐量了。

延时计算主要与flops bound和memory bound 有关。而flops 计算量与batch size和参数量大小正相关，memory 加载仅与参数量大小相关。通信主要是引入两个新条件：latency，吞吐量 throughput。

小批量延时计算公式​

小批量（如1）的 latency 计算公式如下所示。

  • Compute
    • 解释：由于是小批量，所以是memory bound，我们需要用加载所有参数的时间来除以内存带宽，这里我们忽略了kv cache的读取时间，因为kv cache的大小取决于总tokens的数量大小，这里并不好量化。
    • P 是总参数量，2P是bytes量
    • b 代表单位 bytes
    • N 是 GPU 的数量
    • Abm是memory bandwidth
  • Comms
    • 4 是每层需要四次通信（可见上面的模型并行的解释）
    • nlayers 是解码器堆叠数
    • 8us 是目前估计的最小的通信延时（这里作者采用 8 microseconds(10^-6 seconds) per message in Citadel paper for V100 NVLink.）

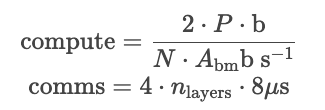
image-20241005024745476

大批量延时计算公式​

对于大批量（如512），latency 计算公式如下

  • Compute 中，我们将总 flops 除以 N 个 GPU 的 flops/s 得到计算延时
    • B 是批量大小
    • 2P (flops)，P是总参数量。2P 是每个参数向量都要进行矩阵乘，对于参数(m,m)，如果参数量为m^2，则其矩阵乘flops为2m^2
    • Af (flops/s) 是单个 GPU 的每秒浮点运算操作，同样在 KV Cache 有详解。
  • Comms 中，用总共需要通信的字节数除以通信吞吐量
    • B 是批量大小
    • b 代表单位 bytes
    • 2 是 float16 中有两个 bytes
    • nlayers 是解码器堆叠层数，需要经过 nlayers 轮计算。
    • 在模型并行中，我们有提及 4(N-1)d_model/N 为一层解码器内的通信数据量，这里把 （N-1）视作 N，得到 4*d_model
    • 所以分子为 2*nlayers*4*d_model bytes
    • Ac (byte/s) 是 GPU 间的通信吞吐量，模型并行中有提及（300GB/s）。

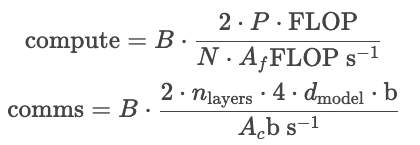
image-20241005034058189

实例：Gopher sized 260B model on 16 GPUs，A100（1.5e12 是内存带宽）​

小batch的延时如下所示，一个token计算延时为22ms，通信延时为3ms

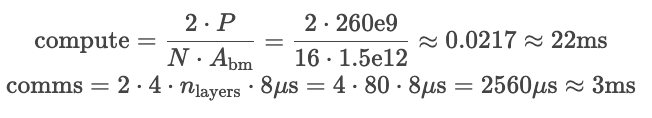
image-20241005042532664

大batch的延时如下所示，从comms可得通信吞吐量为18/512=25us，一个token计算延时为53ms

image-20241005042809108

结论​

因为 comms 和 compute 是并行的，我们选择最高的值作为延时，。需要避免 comms 大于 compute。我们不可能通过无限量地添加 GPU 增加计算能力来从而延时降到最低，comms 会随着 GPU 变多而增大。

虽然计算出来的延时比实验小，因为没有考虑到硬件使用率，没有考虑softmax、addnorm操作的延时等，但演示计算公式有助于思考如何去优化性能。

批次大小 Batch Size​

批量大通常意味着更高的GPU利用率​

batch size 是指在一次推理中同时处理的请求数量。比如，batch size = 4 意味着在一次推理操作中，模型同时处理 4 个请求。request 请求是模型推理过程中输入的 prompt，每个 request 包含的 token 数量可以不同。

  • 在没有达到速度与内存带宽的比值临界点前，更大的批处理大小通常意味着更高的 GPU 计算利用率，从而提高推理效率。

批量大小是影响推理性能（延时）的重要因素，延时计算中提到小批量是memory bound，大批量是flops bound（如下公式所示）。在实践中，我们希望达到flops bound，因为这样可以尽可能利用通信带宽、内存带宽以及flops计算资源。那么，如何找到临界最佳批量呢？

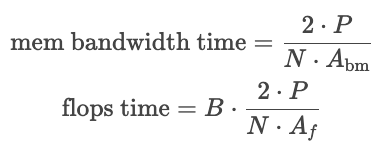
image-20241005044224868

  • 批量大了一开始会有助于达到flops bound，但批量太大了，会使得通信延时增大，反而会增加总体延时。

使用 flops/byte 来统计flops是否大于comms​

在一个编码器层中，总共有四次通信，中间穿插着计算，我们希望每步通信中flops延时长于comms延时。这里用一个奇怪的比值，每bytes通信触发的flops（flops per bytes of comms）来作比较。下表展示了 flops/byte 的估计值

  • 在 A100 中，flops/comms = 312e12/300e9 =1040，所以我们要尽可能让表中最后行flops/byte的值大于1040以追求flops bound，由于每步通信的flops/byte都不同（d_model, 3d_model, 4d_model），如果d_model大小是1024，那每步通信前后都能做到flops bound。

image-20241005114754992

一些结论​

  1. 在API请求少时，batch size会很小，可以把kv cache去掉，来更多地利用flops，因为flops比内存加载更快（？todo => ）

  2. 如果API请求的批量很大，可能最好还是使用允许flops bound的临界值的批量大小，因为这样子可以优化per-request-latency（todo）

    1. 如果是 comput bound，应该用KV Cache减少 compute。如果是 memory bound，应该尽可能使用 compute

  3. 对于像 AlphaCode 这样的推理任务，我们可能希望插入尽可能多的gpu，所以可以尽可能增大batch size。

flops 计算​

下面我们估算Transformer的flops计算量是否是上面所提的2P

Attention

  1. Wk，Wq，Wv 权重，矩阵乘法
    1. W(d_model, d_model), X(1, d_model): 3*2*d_model^2
  2. 计算/拼接 Z
    1. softmax: d_model
  3. Wo 输出映射权重，矩阵乘法
    1. WO(d_model, d_model), Z(d_model, 1): 2*d_model^2

FNN

  1. 全连接层 W1(d_model, 4d_model), W1(4d_model, d_model): 8*2*d_model^2
    1. 中间有 ReLU，可以忽略不计

Others

  1. 在第一层前，有token embedding，有位置编码计算
  2. 在 FFN 中的激活层计算（上面已经提及）
  3. 在FFN后，有layer norm残差连接层，其权重向量为 d_model
  4. 最后一层解码器后，还会有softmax和output token unembedding的工作

这些计算都是向量层级的操作（vector-vector (or even vector-scalar) operations），都是 d_model 维度的而不是d_model^2，即使有100个这样的操作，其总flops计算量也就100M，远远达不到flops计算量的0.1%

All

汇总 d_model^2 级别的操作，我们可以得到 2*n_layers*12*d_model^2，即 2P

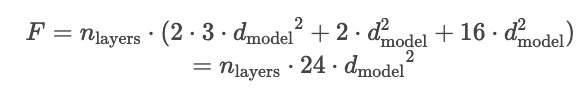
image-20241005123045278

以 52B 参数模型的参数为例，d_model 为 8192，n_layes 为64，flops 约为103B，已经是 52B 的两倍了。

image-20241005123159890

中间的内存成本 Intermediate memory costs​

Data Movement Is All You Need 提到在实际硬件上，模型的操作（如矩阵乘法、layernorm、softmax）会因为数据移动的成本而产生延迟。

虽然通常我们用 FLOPs 来衡量计算复杂度，但对于一些操作（如 softmax），它们的主要性能瓶颈在于内存的读写速度，而不是计算本身。因此，在评估模型的性能时，除了关注计算复杂度，还需要考虑数据移动的延迟（内存带宽）。

the latency for softmax is actually slightly higher than the calculations for qkv (which are a 1/3 of the time). This is a little concerning!

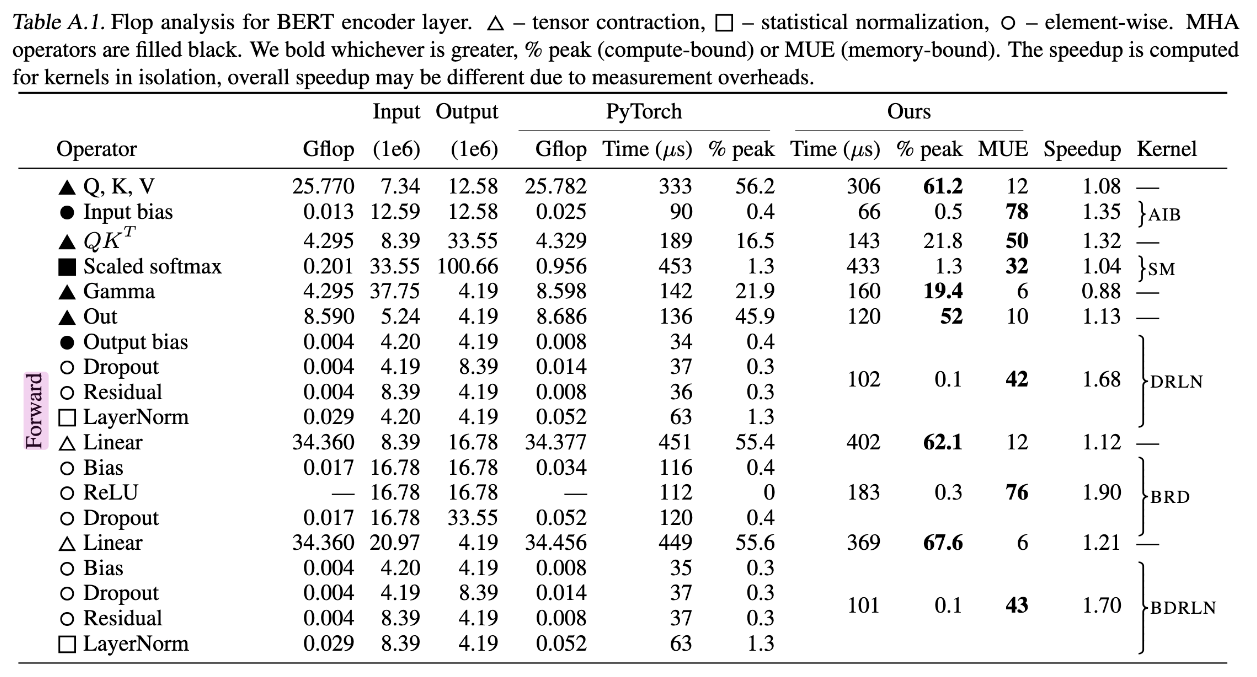
image-20241005125011108

  • the softmax is memory bound, so is the multiplication of qk, ReLU and dropout are also quite expensive.

  • Softmax 的内存操作可以优化，但在现有实现中并不完美。

  • 随着模型规模增加，FLOPs 增速高于内存操作的增速，因此内存受限操作的相对重要性降低。

  • 在更大模型（如 52B 参数）中，中间操作对总推理延迟的影响变得微不足道，约占 5%。

与真实的基准报告作比较 comparing against real beachmarks​

There is a sadly small number of public benchmarks available for model parallel inferencing?

现在公开的 beachmarks 只有 Nvidia FasterTransformer and Microsoft Deepspeed

Use 2 GPUs, I've run a 13B parameter model with FasterTransformer

13B is 40 layers, 40 heads, each of dim 128 for a dim size of 5120

We'll start with a 512 context length, batch size 1 and 10 tokens outputted. For a small batch for one token on 2 GPUs we expect 8.4ms, and about 1ms of comms. For 1 GPU, that would be 16.8ms and 0 comms. (2x40x12x5120^2/1.5e12)

Our empirical result for 1 GPU is 22.0ms, meaning our guess was 76% there.

Question​

  1. 是否考虑到 flops bound 和 memory bound，最佳的推理上下文长度是 208（flops/bytes）？=> reddit 有人回答，optimal context length = （显存大小GPU VRAM - KV Cache）/ batch_size

Reference​

  1. Transformer Inference Arithmetic by kipply 2022
  2. LLM Parameter Counting by kipply 2022
  3. KV Cache Quantization by Hugging Face
  4. Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism