Skip to main content

The Illustrated Transformer (Notes)

  • 注意力机制
  • 适合并行

A High-Level Look​

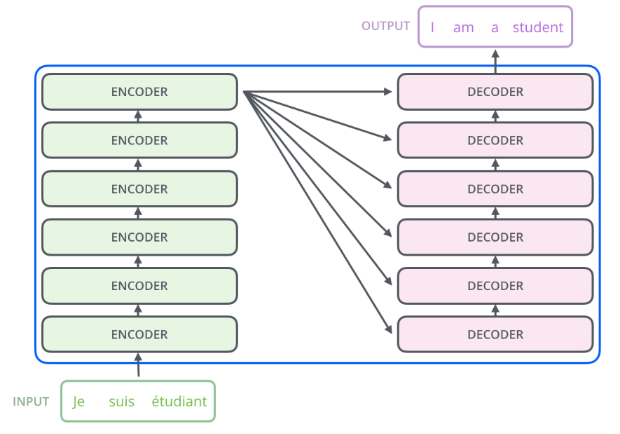
  • 编码器解码器架构，seq2seq
  • 编码部分由一组编码器堆叠组成，解码部分由一组解码器堆叠组成
  • 编码器 = 自注意层 + 前向反馈网络

编码部分由一组编码器堆叠组成，解码部分由一组解码器堆叠组成

image-20240928092031711

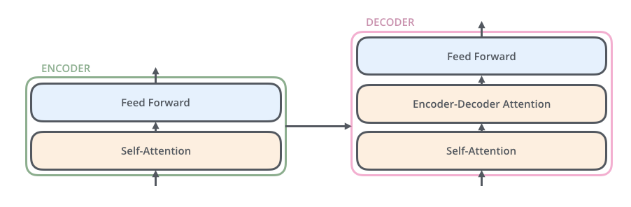
编码器 = 自注意层 + 前向反馈网络

image-20240928092040390

引入 Tensor​

每一个输入单词都被编码成一个向量

image-20240928092229578

一个向量的大小是 512，最底层的编码器负责 word embeddings，之后的编码器只要接收 embeddings 即可。

输入的词向量的序列长度是超参数，通常是训练数据集中最大的句子长度。

编码器​

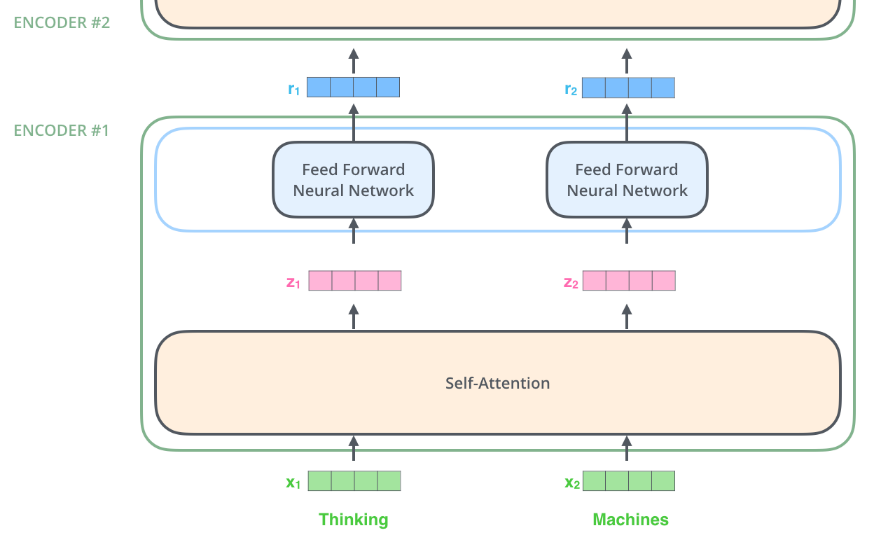
如下图所示，Transformer 的一个关键特性是每个位置的单词有单独的处理路径，也就是可以并行化。

image-20240928101317056

自注意力计算​

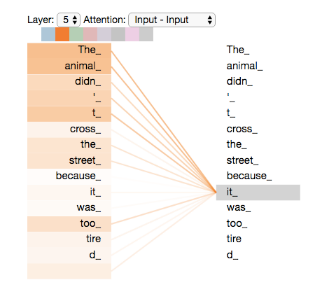
以这句话为例 The animal didn't cross the street because it was too tired，Transfomer 的自注意力模块让模型明白输入中的 it 与 The animal 的相关关系，就像 RNN 中的隐藏状态使得模型学到前后单词的关系。

image-20240928101848972

下面介绍如何用向量计算自注意力

首先需要编码 query，key 和 value

把输入 word 向量 X 通过与参数 W 乘积 XW，编码成 query，key 和 value。此处 word 为 512 长，query, key 和 value 长度为 64。这个大小是多头注意力常见的配置。

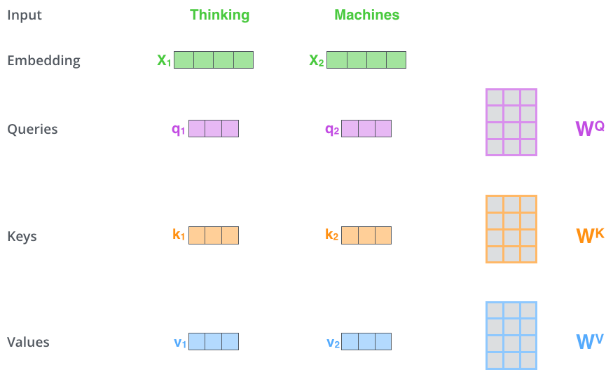
image-20240928104049409

第二步需要计算单词与句子中其他单词的自注意力分数（点积）

如下图中，Thinking 与 Thinking 的自注意力为 q1*k1，与 Machines 的自注意力为 q1*k2

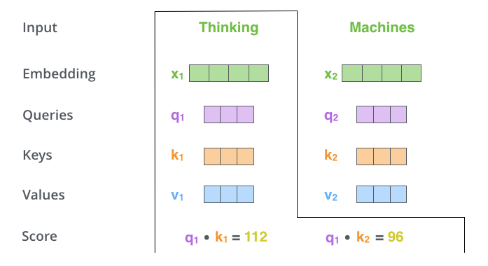
image-20240928104519252

第三步：为了使得注意力分数更稳定，将其除以 8 （词嵌入向量大小 64 的平方根）。

第四步：做 Softmax 计算，得到总和为 1 的正数

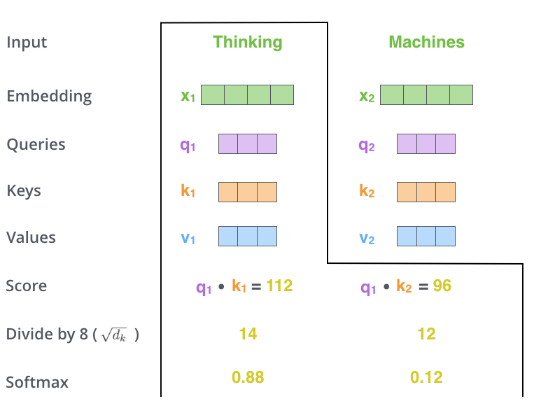
image-20240928104909671

第五步： 各个单词的 Value 矩阵乘Softmax的输出得到加权的 Value，可知注意力权重越大，Value 保留的值也越多。

第六步：把这些分数加起来，所以 Thinking 的总分是 v1*Softmax(q1k1)+v2*Softmax(q1k2)

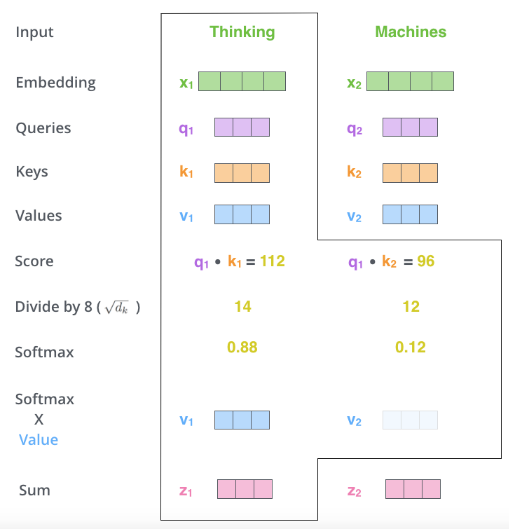
image-20240928110237365

最后，z1，z2 将被送到前馈层中计算。上述的计算实践中都是矩阵计算完成的。

自注意力的矩阵计算​

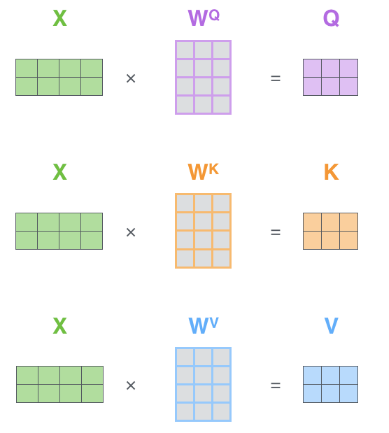
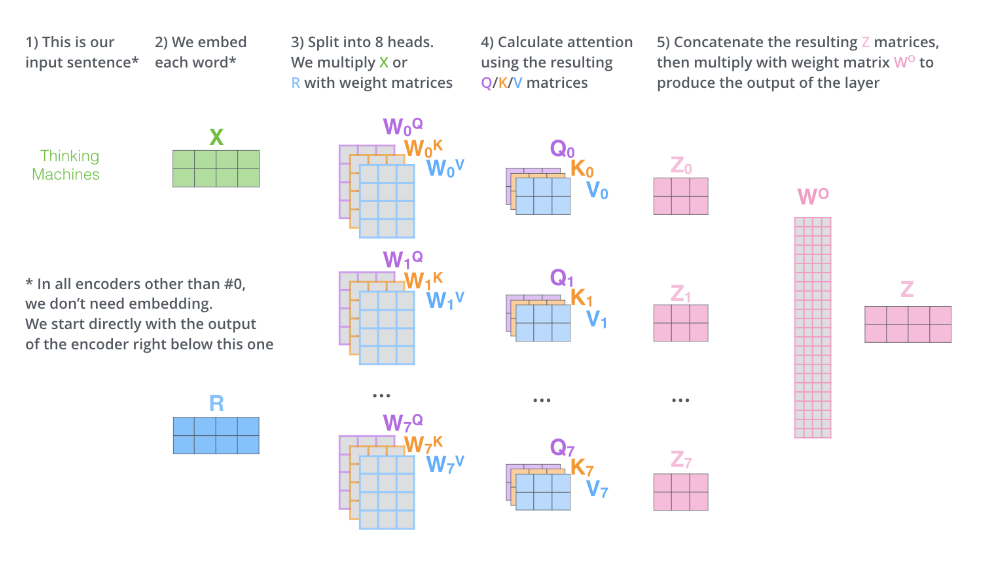
Query，Key 和 Value 的矩阵计算如下图所示，为 (WQ, WK, WV)

image-20240928111350498

第 2 步到第 6 步的计算，可以汇总为下面的公式

  • 开方 dk（dimension of Key vector），由于 key 长度一般为 64，所以开方 dk 为 8
  • 下面 Q 是要计算自注意力的 word，而 K，V 为输入序列每个 word 的
  • KV 是历史，Q 是当前的查询
  • 此处为QxK为点积，Softmax()@V为矩阵乘
    • 这里Q长度为

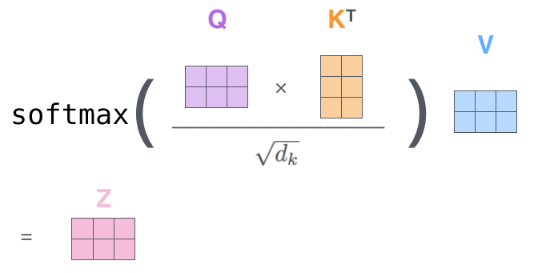
image-20240928110947946

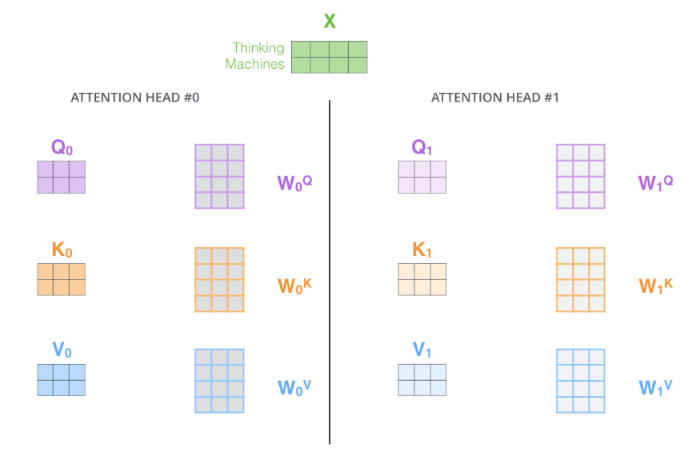
多头注意力​

通过使用多个头，可以

  • 增加对不同位置的关注能力。原始的自注意力中，单词本身的权重很大。如果我们训练 “The animal didn’t cross the street because it was too tired”，可以帮助了解到 “it” 指的是什么。
  • 为注意层提供了多个“表征子空间”（representation subspaces），帮助模型从不同的角度和特征维度处理输入，每个头都有独立的一套 Wq,Wk,Wv 参数

image-20240928112821415

如果有八个头，最终会有 8 个不同的 z。

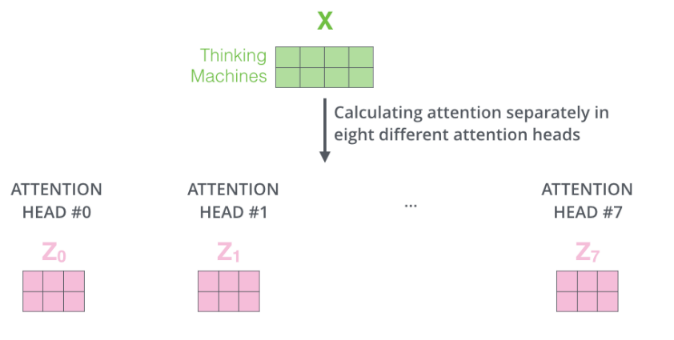
image-20240928113426529

而这会带来一个新问题，自注意力层输出了 8 个 Z 向量，但是 FFNN 前馈层之前只处理一个 Z 向量，怎么解决呢？可以通过

  • 把 8 个 Z 拼接起来得到一个 Z**（输出也是 512）**

    • token 输入是 512

  • 乘以 W 权重，得到的 Z 也是 512

image-20240928114125405

所有的操作可以汇总成下面的图

  • 其中 X 是第一个编码器的输入，第一个编码器需要处理词向量编码。而后续的编码器只需要处理前面的编码器传递过来的 R 即可

image-20240928114635661

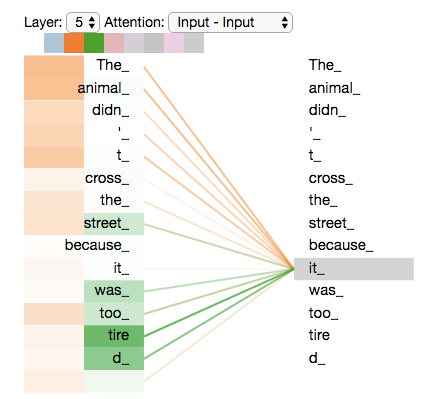
接下来看看单词 it 在两个注意力头中的权重，可以看到 it 在第一个头中与 The Animal 强相关，在第二个头中与 tired 强相关。

image-20240928115142737

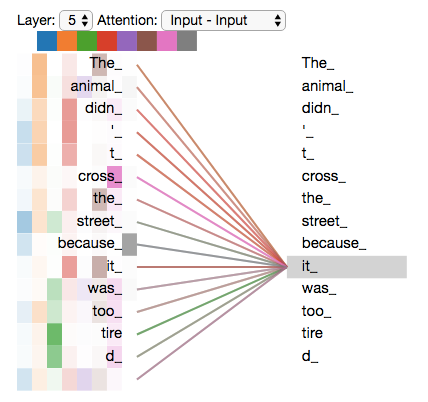
如果把 8 个注意力头放在一起，表示了it对不同词的注意度

image-20240928115229284

使用位置编码来表示序列的 Order​

在第一个编码器编码词向量时添加位置编码，使得编码器能够学习到每个单词的位置及单词间的距离关系。

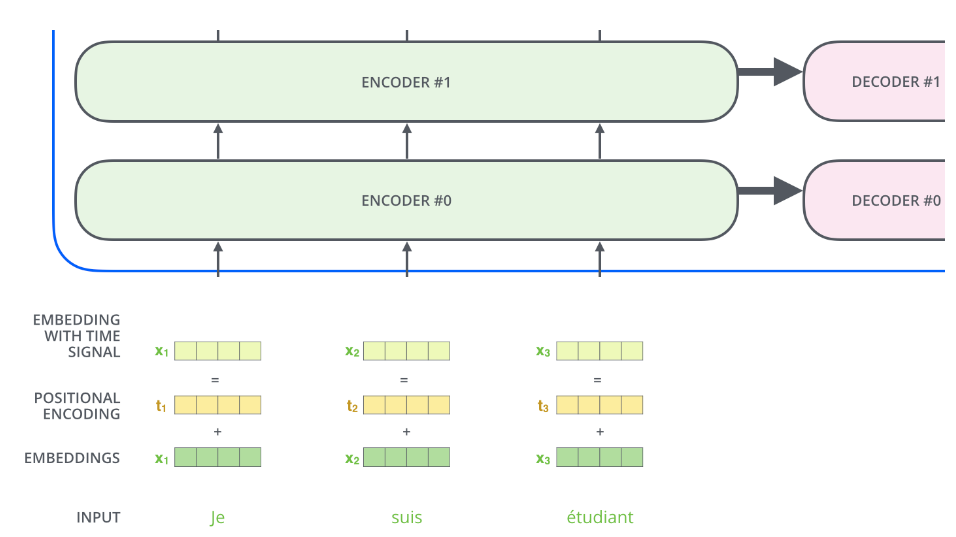
image-20240928122213369

假设词向量的大小为 4，则位置编码也是 4，每个位置有各自的权重

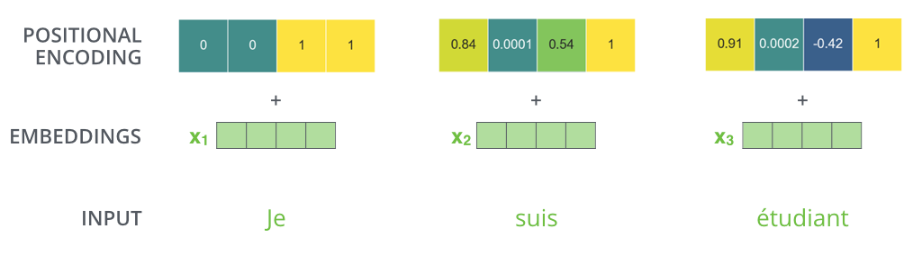
image-20240928122936217

在论文（attention is all you need）中提出了使用 cos 和 sin 函数来做位置编码

下图为对 20 个 512 维的词向量做 sin 和 cos 位置编码的拼接图，可以看到，有 20 行 512 位数据，并且输出的图像展示了权重编码的规律。

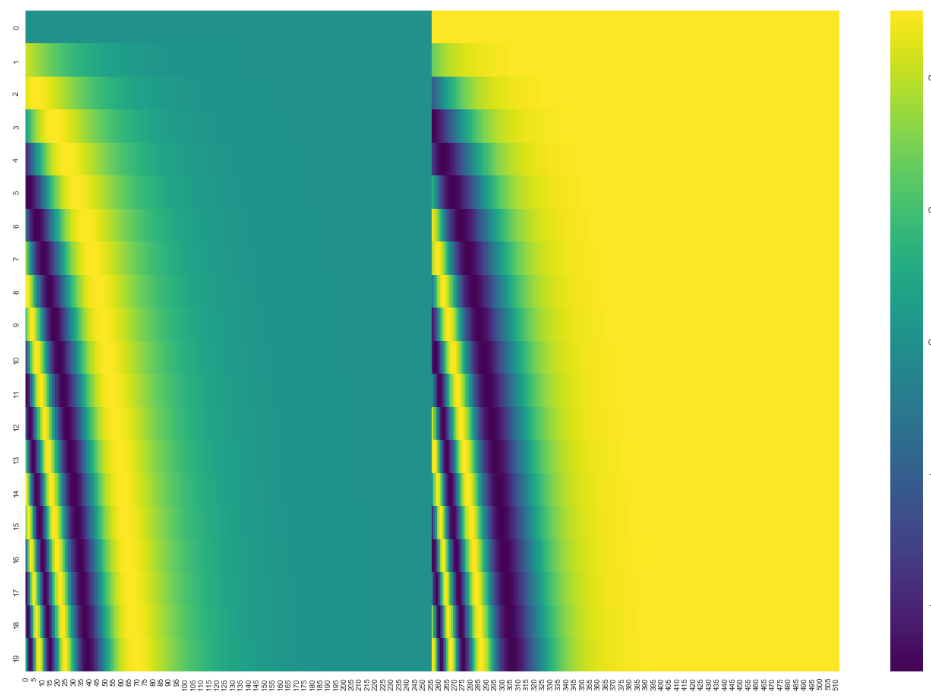
image-20240928123501968

残差网络​

在编码器中的每层网络（自注意力，FFNN）内还有两个重要成分

  • 残差连接（Redisdual）
  • 层规范（Layer Norm）

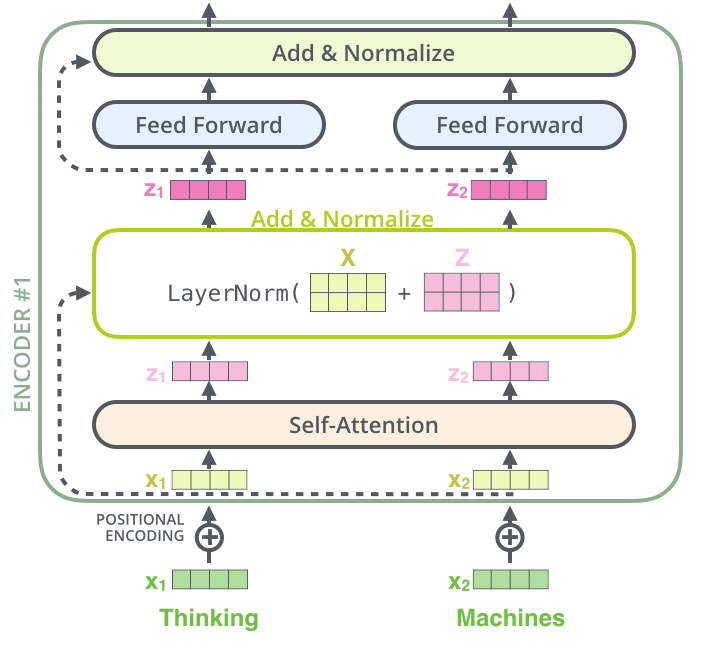
image-20240928123911434

两个的编码器解码器堆叠的可视化架构如下

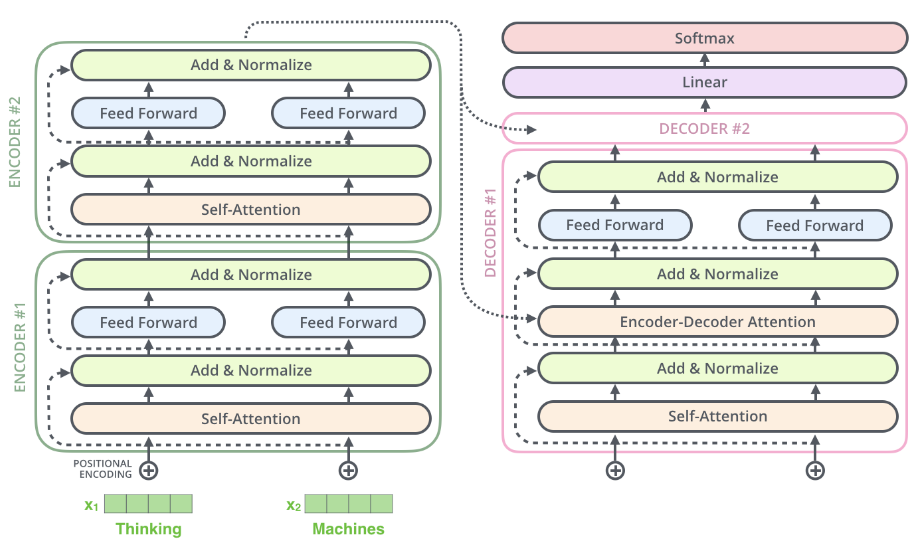
image-20240928124132927

解码器​

  • 编码器的输出被转换成为 K V 向量，被用到每个解码器中的编码解码自注意层（encoder-decoder-attention），帮助解码器关注到输入序列中合适的位置。
    • 编码器每次的输入只能和之前的生成 word 计算自注意分数，所以要忽略后面位置的编码。可以通过在 Softmax 前添加未来位置的掩码（masking future positions bysetting them to -inf）来解决
    • 解码器和编码器的自注意基本类似，但解码器的 K V 向量来自解码器，只有 Q 向量来自于前面的解码器。
  • 在下图中
    • 一开始输入开始符号 <start> （TODO）
    • 输入 I 添加第一个位置的位置编码后，输入解码器
    • 解码器生成 am
    • 把 am 添加第二个位置的位置编码后，输入解码器
    • 解码器生成 a
    • 依此类推，直到解码器生成标识结束的字符，如 <end>

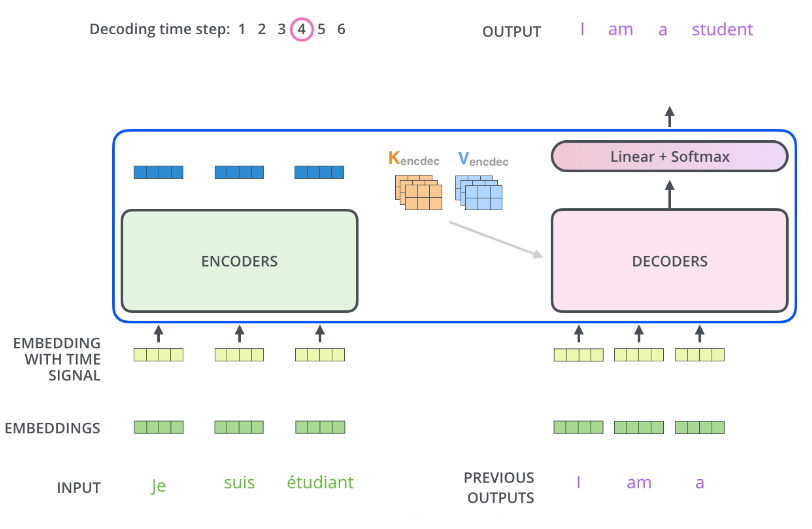
image-20240928124708185

Linear 层与 Softmax 层确定输出词​

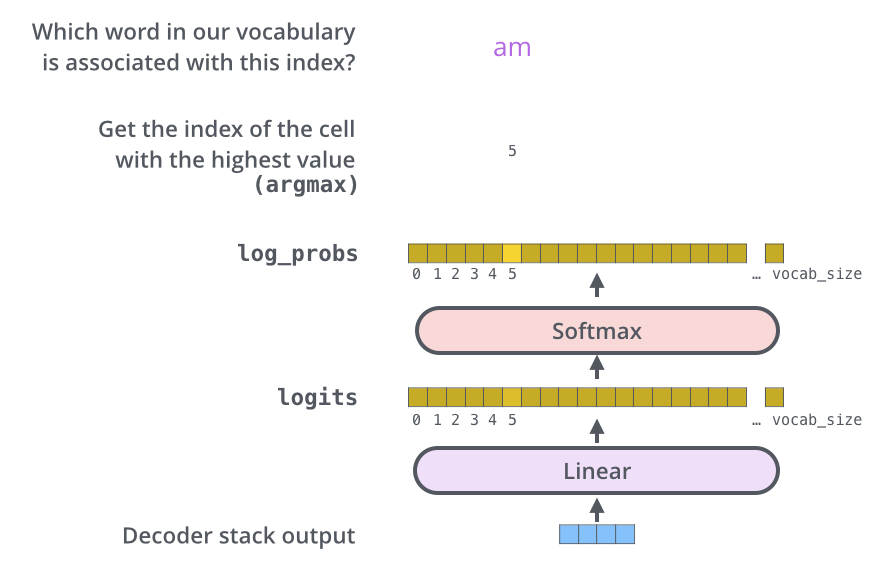
问题：解码器生成的词向量是浮点数，如果我们要输出的是单词时，并不能确定输出的单词。

所以我们需要

  • Linear 全连接层，根据解码器输出的向量，生成一个 logits 向量，其长度为词汇表（Vocabulary）的长度 vocav_size
  • Softmax 层，把分数转化为 Softmax 概率（所有的概率为整数，合为1），最高概率的格子对应的单词被选中（在下图中也就是 位置5 的 am）

Vocab_size，词表长度，比如我们的输出有 1000 个英文单词，则词表长度为 1000

image-20240928130010989

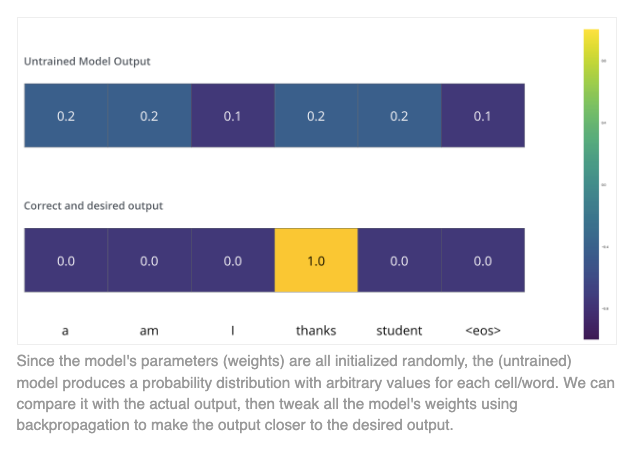
训练​

监督学习，通过目标输出来计算。

损失函数​

通过计算目标与输出的距离，并减少这个距离实现。

For more details, look at cross-entropy and Kullback–Leibler divergence.

  • 不用花特别多时间

image-20240928130817594

Todo​

计算​

Todo

  • Cross Attention 层
  • 现在是纯 decoder 的结构，decoder only。为了计算效率的平衡，gpt 目前的架构，更好 scale up，for pipeline，etc
  • FFN 的大小是多少？
  • (m*4m + 4m*m) = 8m^2
  • (1, 512)
    • WK (512, 64) * 8 * 3 = 3m^2
    • WZ (512, 512) = m^2
    • Softmax 也算运算
  • seq(t1, t2, t3)
  • 衡量指标：number of flops/number of weights bytes
  • 加速 FNN 层 => 加大 batch
  • 加速 self-attention 层 => 序列计算关系，不太能并行
  • X1 (1, 512)
  • WQ (512, 64)
    • 64*8=
  • Q1 (1, 64) = XW = ``
  • K (1, 64) * 8 = 512 float16 * 2 => 1024 bytes * n(seq_len)
  • V (1, 64)
  • Z

Transformer Inference Arithmetic​

https://kipp.ly/transformer-inference-arithmetic/

Reference​

  1. Word Embedding
  2. The Annotated Transformer(Pytorch Implementation)
  3. Tensor2Tensor notebook Transformer Implementation