Skip to main content

DL/ML Common Concept

模型相关

  • 损失函数
  • 度量模型，损失函数
  • 训练阶段
    • 优化算法
      • 解析解
      • 梯度下降（训练模型，优化损失函数）
    • 模型选择
    • 欠拟合和过拟合
    • 权重衰退
    • 暂退法（Dropout）
    • 数值稳定性和模型初始化
    • 环境和分布偏移

概念

  • 最大似然估计
  • 神经网络图

img

最大似然估计​

假设有一个模型，用 P(X|θ) 表示，其中 X 是观测数据，θ 是模型参数。这里 P(X|θ) 表示给定参数 θ 时，观测到数据 X 的概率。当我们观测到 X 希望估计未知参数 θ 时，称 L(θ|X) 为似然函数（likelihood function），有 P(X|θ)=L(θ|X)。

最大似然估计

  • 似然表示某个模型参数在给定观测数据的情况下解释数据的能力，似然函数取得最大值表示相应的参数能够使得统计模型最为合理。

假如掷硬币正面朝上的概率是 PH，我们掷硬币三次，两次正面朝上，一次反面朝上的似然函数如下，从函数图像中可以得知，PH 为 2/3 时达到最大似然函数值，所以我们可以猜测 PH 为 2/3

image-20240919011809337

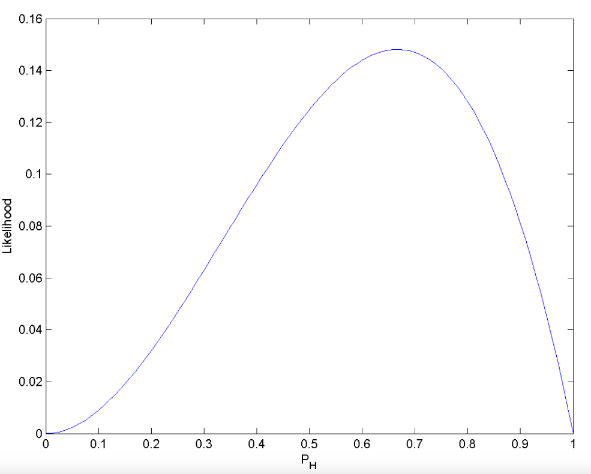
image-20240919012436134

神经网络图​

深度学习从业者喜欢绘制图表来可视化模型，可以将线性回归模型描述为一个神经网络。只显示连接模式，即只显示每个输入如何连接到输出，隐去了权重和偏置的值。

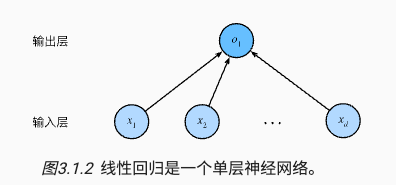
image-20240919014810350

图中要点

  • 输入层为 x1,x2,...,xd 为 d 维，输出层 01 为 1 维
  • 统计网络层数时会忽略输入层，所以这个神经网络是 1 层
  • 这是一个全连接层（fully-connected layer）或称为稠密层（dense layer），即每个输入与每个输出相连

数学术语​

  1. 极值点（arguments of the maxima/minima，分别缩写为arg max/arg min或argmax/argmin）是使函数输出值取得极值的输入点。

特征工程​

  • 特征描述子：SIFT，SURF
  • 视觉词袋（类）
  • 最后用SVM