物理时钟，Lamport 时钟与 Vector 时钟 Physical Clock, Lamport Logical Clock, and Vector Clock

Time, Clock, and Ordering of Event

Ordering of Event

Why need to order event?

• In real life, some things should happen in order.
• For example,
  • News should be corrected before being released.
  • Membership card is only activated after the user paid
  • Multiple updates of content should happen in order.
  • The privacy should be updated before posting

How to order event?

• Label each event with its physical time

Physical Lock

Approach #1 synchronization

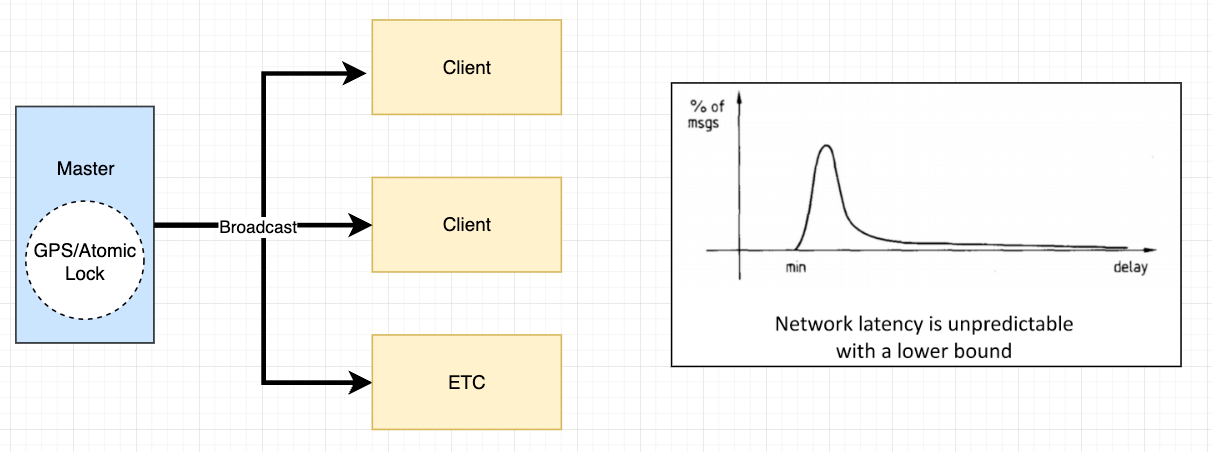
Beacon-based approach

1. Designate server with GPS/atomic clock as the master
2. The master periodically broadcasts the time to clients. Clients resets the time upon receipt
3. Problem: the unstable latency in event sending and receiving

Approach #2 Interrogation-based protocols

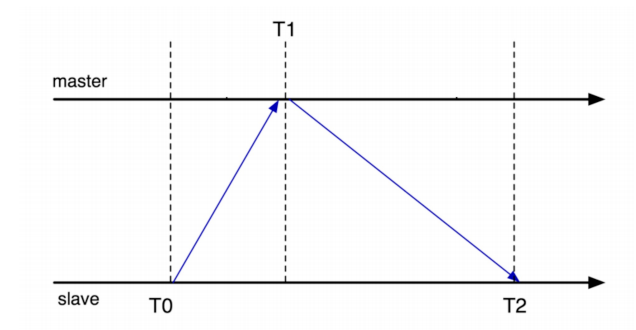
1. Client queries server
2. Time = T1 + (T2-T0)/2
3. Multiple samples, average over several servers; throw out outliers
4. Take into account the clock rate skew
5. Protocols:
   1. NTP (Network Time Protocol), used in server sync, log records, etc.
   2. PTP (Precision Time Protocol), used in electricity network, financial trading system, et.

Physical Lock Problem

• Physical lock is not accurate.
• Physical lock is not the same among multiple machines.

How to order events without physical clock?

Happens-before relationship

1. Happens-before relationship captures logical (causal) dependencies between events.
2. For example, Cooking before Eating; Eating before Sleep.
3. (Irreflexive) partial ordering: ->
   1. a -/-> a, (an event cannot happen before itself)
   2. a -> b, then b -\->a, (if a happens before b, b cannot happen before a)
   3. a -> b, b -> c then a -> c, (if a happens before b and b happens before c, then a happens before c)

Irreflexive Explanation

Irreflexive means that no element is related to itself. In the context of happens-before relationships, it means an event cannot happen before itself (a -/-> a).

Partial Ordering Explanation

A partial ordering is a mathematical concept used to describe a set of elements where some pairs of elements are comparable, but not necessarily all. In the context of happens-before relationships, it helps define how events are related in terms of their order.

Happens before In distributed systems

1. Processes
2. Messages
3. Events
   1. Send msg; Receive msg; Event happens

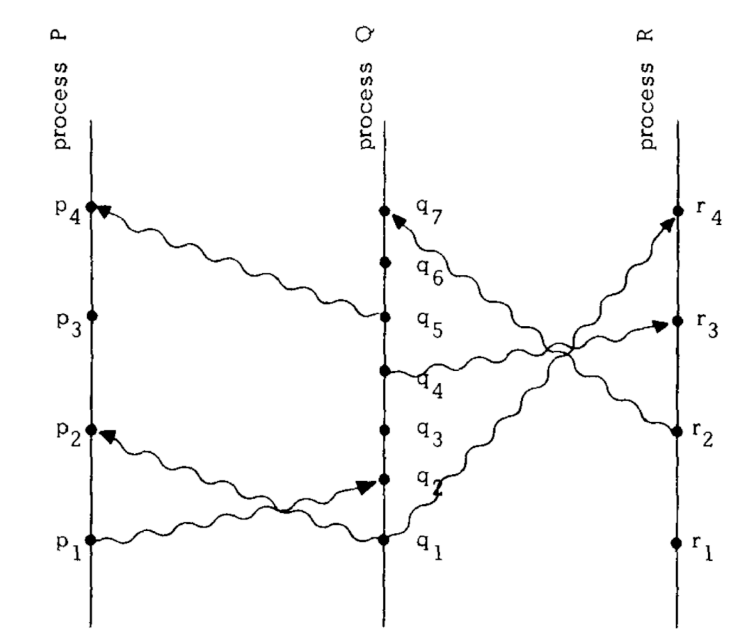
Properties

1. Happends-before

   1. Within a process, a comes before b, we have a -> b

   2. a -> b means b could have been influenced by a

2. Transitivity

   1. if a -> b and b -> c then a -> c

3. Concurent

   1. a -/-> b and b -/-> a: events are concurrent
   2. Concurrent means: No one can tell whether a or b happened first.

Example

1. Events with happens-before relationship
   1. Cooking before Eating,
   2. Eating before Sleeping,
   3. Washing before Sleeping
2. Transitivity: Cooking Before Sleep
3. Concurent: Washing is concurrent with Eating, we cannot determine the order based on limited given happens-before infomation.

Lamport Logical Clock

Goal

We need to mark each event with timestamp C to preserve the happens-before order of events.

if a -> b, then C(a) < C(b)

Implementation

1. Keep a local clock T on each process
2. Increment T whenever an event happens
3. Send clock time on all messages as Tm
4. On message receipt: T = max(T, Tm) + 1

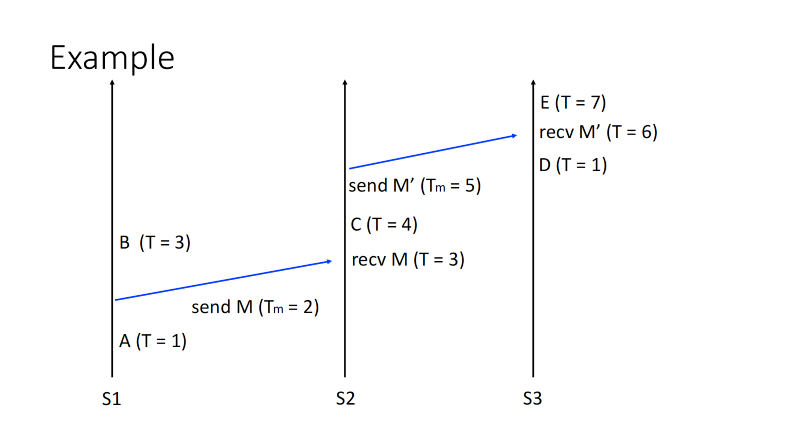
Use the logical clock to form a total ordering

The following is just to define a new relation: => based on C() < C()

大白话来讲，如果 a 的时间戳比 b 小，我们可以说 a => b。如果 a 发生在 b 之前，即 a -> b，我们可以说 a 的时间戳一定比 b 小， 即a => b。但反之不成立。

1. If C(a) < C(b), then a => b
2. If C(a)==C(b), the processID of a and b shoudl be different
3. a->b means a=>b
   1. In converse, a=>b, i.e. C(a)<C(b) doesn't mean a->b. For example, the event B(T=4) ie concurent to D(T=1), we cannot said D -> B based on the C(D) > C(B)

Logical Lock Problem

We cannot tell the ordering of events with conccurrent logical lock

1. When a -> b, then C(a) < C(b) But in converse, if C(a) < C(b), it doesn't mean a -> b, they could also be concurrent in different processes
2. For other concurrents cases which not even C(a) < C(b), we cannot tell the ordering of event as well based on physical lock.

Vector Clock

Vector clock will resolve the logical lock problem.

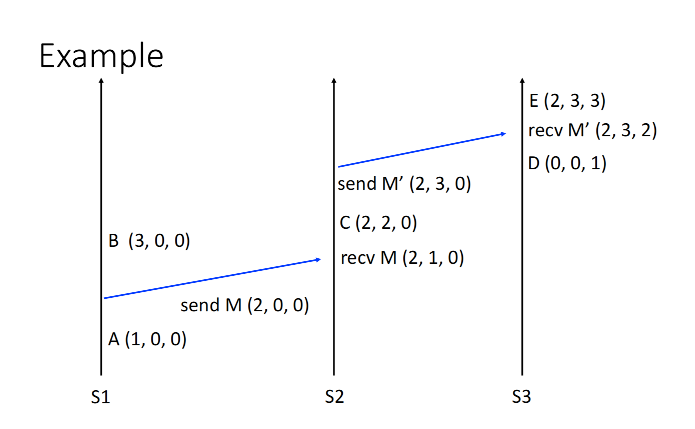
Rules

1. Clock is a vector, its length is n, i.e. the number of nodes.
2. On node i, increment C[i] on each event
   1. For exmaple
      1. Node #0 with vector lock (3, 5, 2);
      2. After a event happen: (4, 5, 2)
3. On receipt of a message with clock Cm on node i:
   1. Increment C[i]
   2. For each j != i, C[j] = max(C[j], Cm[j])
      1. For example:
         1. Node #0 with vector lock (4, 5, 2) receives a message (2, 7, 0), its vector lock is updated to(5, 7, 2)

Properties

1. Happens before
   1. If Cx[i] <= Cy[i] for all i, and there exists j such that Cx[j] < Cy[j]
      1. That means Cx happens before Cy
2. Concurrent
   1. For two vectors x and y, if Cx[i] < Cy[i], and Cx[j] > Cy[j] for some i and j

Others

TCP ensures the msg received is the newest and latest in the msg tunnel between a and b

Reference

1. NUS CS5223 Distributed System Course
2. Time, Clock, and the Ordering of Events in a Distributed System
3. Designing Data-Intensive Applications